Let f be a function defined by: ?
Let f be a function defined by:
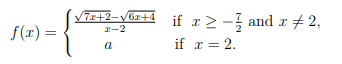
State the domain of "f" and find the value(s) of a for which "f" is a continuous function.
Let f be a function defined by:
State the domain of "f" and find the value(s) of a for which "f" is a continuous function.
1 Answer
The Domain of the Function is:
or
The value of a is
Explanation:
So the first thing the question is asking is "What is the domain of the function?" The domain of a function is the list of
The piecewise physically limits our domain, but that's not actually the domain, since we have a square root with an x in it. Since we're going to be ignoring imaginary numbers (otherwise the doman would be
In this case,
or
The next question asks "Find the value of
So how do we do that? Well we have different ways of going about this. The first, and simplest, is to graph the function and see what happens at the value.
graph{(sqrt(7x+2)-sqrt(6x+4))/(x-2) [1.6815, 2.2657, -0.0507, 0.2413]}
As we can see, the function clearly approaches
I want to rationalize the numerator, so that I get rid of the square roots up there. So I'll multiply by the conjugate.
Now, let's simplify it.
Now, we can combine like terms and simplify even further.
This is perfect! Now we can cancel out the x-2 on the top and bottom, thus eliminating the hole at
Now, just plug in 2, and get:

