A triangle has corners at #(2 , 6 )#, #(4 ,7 )#, and #(1 ,3 )#. What is the radius of the triangle's inscribed circle?

Question

1734 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-02T12:01:33

Radius of the Incircle is #r_i = A_t / s = 3.46 / 4.82 ~~color(green)( 0.72#

Given #A (2,6), B(4,7), C (1,3)#

To find the radius of the Incircle.

Using distance formula between B, C

#a = sqrt((4-1)^2 + (7-3)^2) ~~ 4.24#

Similarly, #b = sqrt((2-1)^2 + (6-3)^2) ~~ 3.16#

#c = sqrt((4-2)^2 + (7-6)^2) ~~ 2.24#

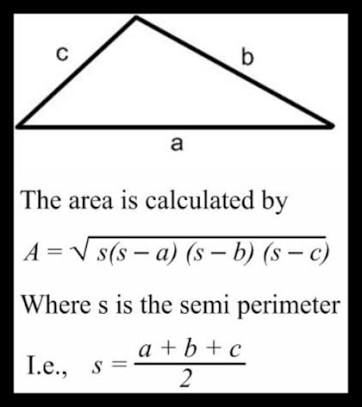
Semi perimeter of the triangle

#s = (a+ b + c) / 2 =(4.24 + 3.16 + 2.24)/2 = 4.82#

Area of triangle, knowing three sides
enter image source here

#A_t = sqrt(s (s-a) (s - b) (s - c))# where s is the semi perimeter.

#A_t = sqrt(4.82 * 0.58 * 1.66 * 2.58) ~~ color(brown)(3.46#

enter image source here

Inradius #r_i = A_t / s = 3.46 / 4.82 ~~color(green)( 0.72#