Question

A triangle has corners at `(5 ,7 )`, `(3 ,9 )`, and `(4 ,6 )`. What is the area of the triangle's circumscribed circle?

Answer 1

Area of the circumscribed circle is

`A_c = pi * R^2 ~~ 7.84` sq units

Explanation:

Steps :
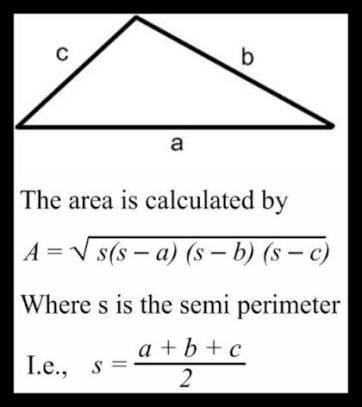
1. Find the lengths of the three sides using distance formula
`d = sqrt((x2 - x1)^2 + (y2 - y1)^2)`

1. Find the area of the triangle using formula
   `A_t = sqrt(s (s - a) (s - b) ( s - c))`

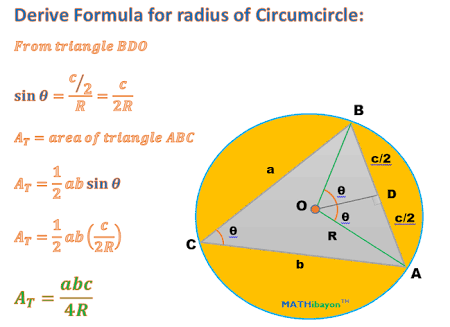
1. Find the area of circum radius using formula
   `R = (abc) / (4A_t)`

1. Calculate area of the circumcircle using formula
   `A_c = pi R^2`

`a = sqrt((3-4)^2 + (9-6)^2) ~~3.16`

`b = sqrt((5-4)^2 + (7-6)^2) ~~ 1.414`

`c = sqrt((5-3)^2 + (7-9)^2) ~~ 2.83`

`s = (a+b+c)/2 = (3.16+1.414+2.83)/2 ~~ 3.7`

`A_t = sqrt((3.7 (3.7-3.16) (3.7-1.414) (3.7-2.83)) ~~ 2`

Radius of the circumscribed circle is

`R = (abc) / (4 A_t) = (3.16*1.414.2.83)/ (4 * 2) ~~ 1.58`

Area of the circumscribed circle is

`A_c = pi * R^2 = pi * 1.58^2 ~~ 7.84` sq units