Question

A triangle has corners at `(7 , 9 )`, `(3 ,7 )`, and `(1 ,8 )`. What is the radius of the triangle's inscribed circle?

Answer 1

Radius of inscribed circle `r_i = A_t / s = 44.72 / 6.4 = color(purple)(6.99`

Explanation:

Steps :
1. Find the lengths of the three sides using distance formula
`d = sqrt((x2 - x1)^2 + (y2 - y1)^2)`

1. Find the area of the triangle using formula
   `A_t = sqrt(s (s - a) (s - b) ( s - c))`

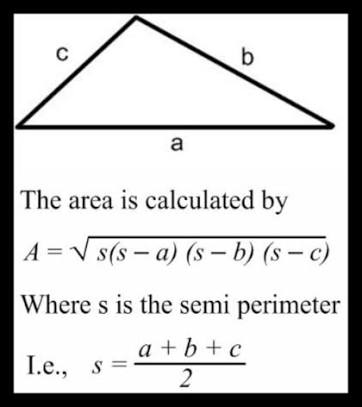
1. Find the semi perimeter of the triangle

`s = (a + b + c) / 2`

1. Find the area of circum radius using formula
   `r_i = A_t / s`

`a = sqrt((3-1)^2 + (7-8)^2) = 2.24`

`b = sqrt((7-1)^2 + (9-8)^2) = 6.08`

`c = sqrt((7-3)^2 + (9-7)^2) = 4.47`

`s = (2.24 + 6.08 + 4.47) / 2 = 6.4`

`A_t = sqrt(6.4 * (6.4-2.24) ( 6.4 - 6.08) (6.4 - 4.47)) = 44.72`

`r_i = A_t / s = 44.72 / 6.4 = color(purple)(6.99`