Question

How do you prove that a shape is a kite?

Answer 1

Kite properties :
Two pairs of sides are of equal length.
One pair of diagonally opposite angles is equal.
Only one diagonal is bisected by the other.
The diagonals cross at 90°

Explanation:

Properties of a kite :

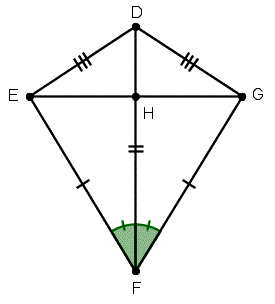
1. Two pairs of adjacent sides are equal.
   `EF = GF, ED = GD`

2. Hence diagonal FD is the angular bisector of angles `hatF, hatD`

3. Diagonals intersect at right angles.
   `FD` perpendicular `EG`

4. Shorter diagonal is bisected by the longer diagonal.
   `EH = HG`

5. Only one pair of opposite angles is equal.
   `hatE = hatG`

All the above 5 conditions are to be satisfied for a quadrilateral to be called a KITE