How do you use integration by parts to evaluate the integral #2xsin(x)dx#?
3 Answers
Mar 3, 2018
I tried this:
Explanation:
Have a look:
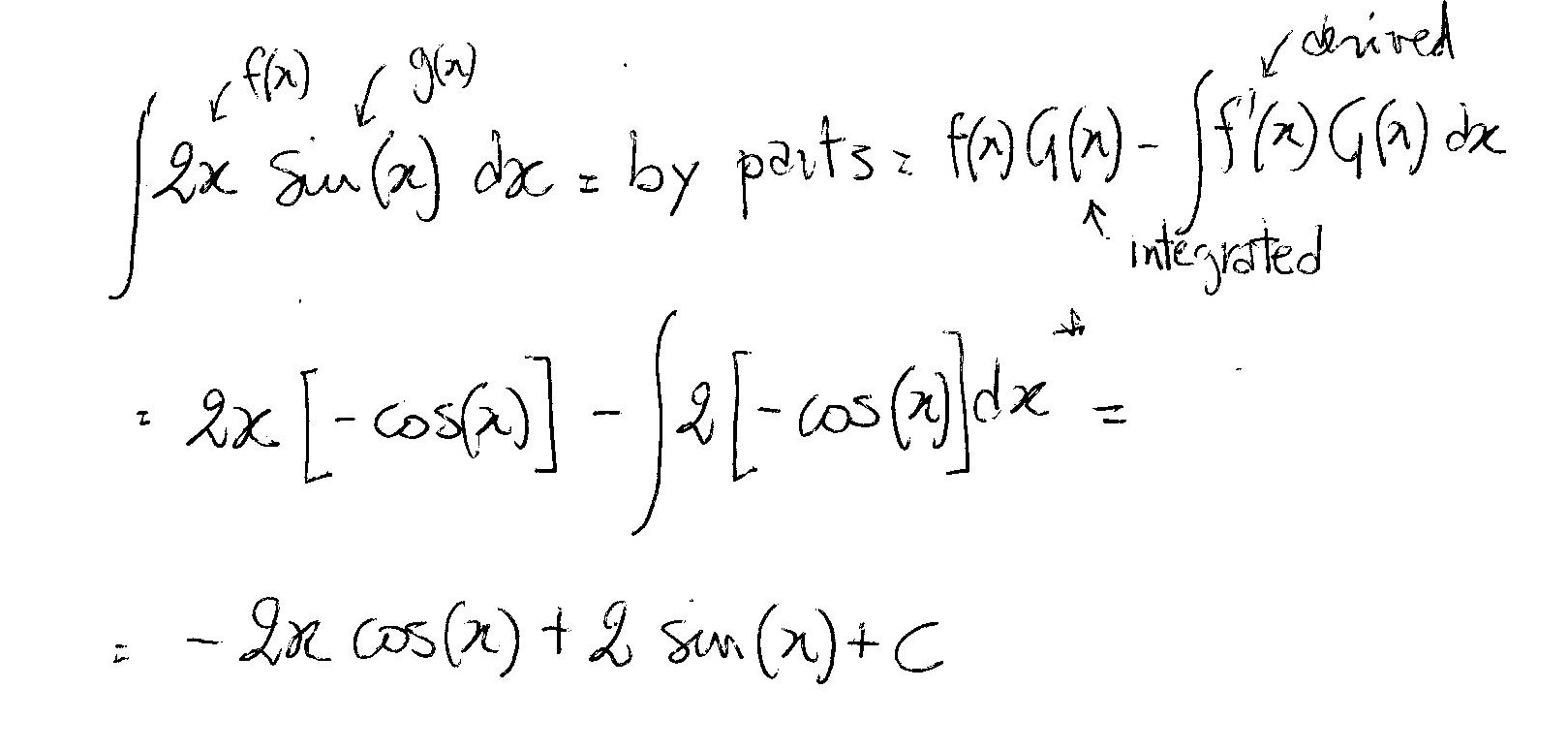
Mar 3, 2018
Explanation:
We have
Take the constant out:
According to integration by parts, where
Here,
So we have:
Add the constant of integration:
The answer.
Mar 3, 2018
Explanation:
Method of Integration by Parts:
Let,
So,



