Question

Hlo friend. what is sum of this terms?1+2+3+4+5+6.........infinty According to Ramunanjan the sum is -1/12

Answer 1

Yes it is `-1/12`

Explanation:

This result sounds really crazy, we know that `S_n=1+2+3+4+....+n=(n (n+1))/2`

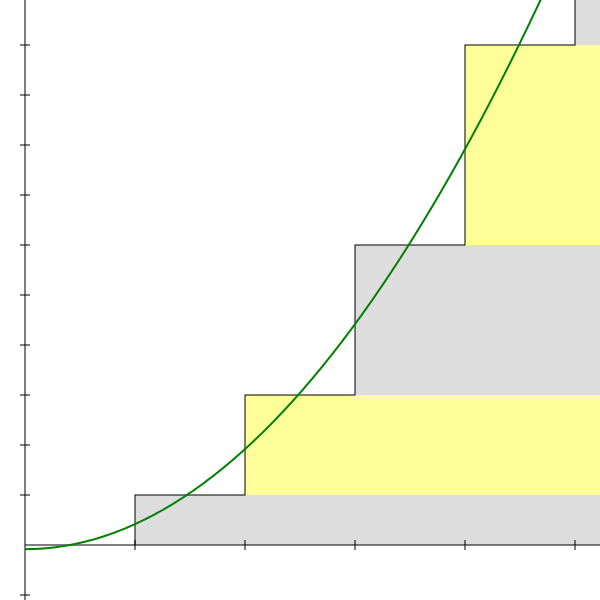
So, as we increase value of n the sum diverges more and more but sum of first infinite natural numbers converges on the negative side of the axis at `-1/12` , everybody could think that the sum would tend to be infinite but infact it doesn't.

[Diverges and converges here mean to convey that if you plot a `xy` graph of given series with number of terms on x axis and sum of y axis , as you increase 'n' y coordinate tends to become more and more larger butif we continue to plot the graph till infinity, which though is impossible, we'll get y-coordinate as `-1/12`]

Here's the proof

Consider
`S_n=1-1+1-1+1-1.......`

If we add some brackets we notice that sum of this series would be

`S_n=(1-1)+(1-1)+(1-1)+.....`

`S_n=0+0+0+0....=0`

But if we just change position of brackets

`S_n=1-(1-1)-(1-1)-(1-1)...`

`S_n=1-0-0-0-0-0....=1`

So, we take the average
`S_n=1/2`
Alternate proof, this is better one.
`S=1-1+1-1...`
`1 - S = 1 - (1 - 1+1-1+1-1+1-1......)`
`1 - S = 1 - 1 + 1 -1 + 1.....`
therefore, `1 - S = S`
therefore, `1 = 2S`
`S = 1/2`

Now consider
`S_(n')=1-2+3-4+5-6+7-8....`

Just add `S_(n')` to itself

`S_(n')=1-2+3-4+5-6...`
`S_(n')=" " 1-2+3-4+5...`

(we have shifted the numbers to little right, because the sum is like `1-(2-1)+(3-2)....` for a finite series this method is invalid, here we are adding `n^(th)` term with `n+1^(th)` term with whatever signs they have before them.)

`2S_(n')=1-1+1-1+1-1...=S_n=1/2`

`S_(n')=1/4`

Now, our main series
`S_(n'')=1+2+3+4+5....`

Subtract `S_(n')` from this series.

`S_(n'')=" "1+2+3+4+5+6....`
`-S_(n')=-1+2-3+4-5+6`

`S_(n'')-S_(n')=4+8+12+16...`

`S_(n'')-1/4=4 (1+2+3+4...)`

`S_(n'')=4S_(n'')+1/4`

`S_(n'')-4S_(n'')=1/4`

`-3S_(n'')=1/4`

`color (green)(S_(n'')=1/4*1/(-3)=-1/12)`

Watch the following videos

Answer 2

The sum diverges, but Ramanujan summation associates the value `-1/12` with the divergent sum.

Explanation:

The sum `1+2+3+...` diverges.

The Ramanujan sum of `1+2+3+...` is `-1/12`

Ramanujan found a method of associating finite values with divergent sums.

In his notebook he wrote a short derivation along the lines of:

`color(white)(c - )color(white)(1)c = 1 + 2 + 3 + 4 + 5 + color(white)(0)6 + ...`

`color(white)(c - )4c = 0 + 4 + 0 + 8 + 0 + 12 +...`

`c - 4c = 1 - 2 + 3 - 4 + 5 - color(white)(0)6 +... = 1/(1+1)^2 = 1/4`

`:. c = -1/12`

If you gave this as a serious attempt at a proof of the value of the sum to any self-respecting mathematician who had not encountered it they would probably laugh. It involves various disallowed operations which essentially boil down to subtracting infinity from infinity.

How did Ramanujan arrive at this particular sequence of manipulations? It is not stable, in the sense that shifting one of the divergent sums one place to the left or right messes up the arithmetic. However, Ramanujan did have some more sophisticated ways of justifying his choices.

There are other ways of arriving at an association between `1+2+3+...` and `-1/12`. In particular, note that the Riemann zeta function is defined (where it converges) by:

`zeta(s) = sum_(n=1)^oo n^(-s)`

This sum only converges (in the conventional sense) when the real part of `s` is `> 1`. However, the Riemann zeta function can be analytically continued to give values for other values of `s`. In particular `zeta(-1) = -1/12`.

If we put `-1` in the previous formula for `zeta(s)` we get our divergent sum `1+2+3+...`.