Question

How do you verify csc^2xcot^2x+csc^2x=csc^4x ?

Answer 1

Take `csc^2(x)` common then it becomes:

`csc^2(x)`(1+ `cot^2(x)`)

which is equal to `csc^4(x)`

Explanation:

Basic trigonometric identities

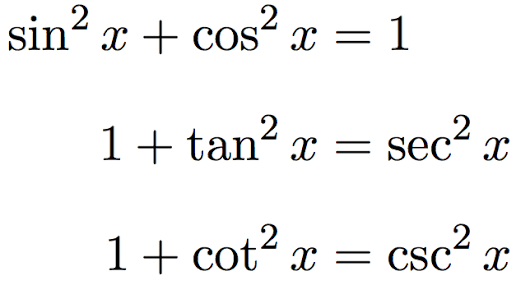
To prove `(csc^2x cot^2x + csc^2 x) = csc^4 x`

Taking common term `csc^2 x` on L H S out,

`=> csc^2 x ( 1 + cot^2 x)`

But `csc^2 x = 1 + cot^2 x` (Trigonometric identity.)

Hence `=> csc^2 x * csc^2 x = csc^4 x = R H S`

Q E D.

Answer 2

It is given that, `csc^2xcot^2x+csc^2x=csc^4x`

`LHS=>1/sin^2x* cos^2x/sin^2x + 1/sin^2x`

`cos^2x/sin^4x + sin^2x/sin^4x`

`(cos^2x + sin^2x)/sin^4x`

`1/sin^4x = csc^4x`; [as we know `color(red)(sin^2x + cos^2x = 1`]