How to sketch this trigonometry graph?

enter image source here

2 Answers
Narad T.
Mar 4, 2018

See the explanation below

Explanation:

The sinus function is

#-1<=sinx<=1#

Therefore,

#-1<=sin(1/3theta)<=1#

And

#-3<=3sin(1/3theta)<=3#

When, #theta=0#, #=>#, #3sin0=0#

When, #theta=pi#, #=>#, #3sin(pi/3)=3/2#

When, #theta=3/2pi#, #=>#, #3sin(1/2pi)=3#

When, #theta=2pi#, #=>#, #3sin(2/3pi)=3/2sqrt3#

When, #theta=3pi#, #=>#, #3sin(pi)=0#

When, #theta=4pi#, #=>#, #3sin(4/3pi)=-3/2sqrt3#

When, #theta=9/2pi#, #=>#, #3sin(3/2pi)=-3#

When, #theta=5pi#, #=>#, #3sin(5/3pi)=-3/2sqrt3#

When, #theta=6pi#, #=>#, #3sin(2pi)=0#

Now you can sketch the curve,

graph{3sin(1/3x) [-1.67, 18.33, -4.24, 5.76]}

Sean
Mar 6, 2018

Please see below.

Explanation:

.

The answer to you question about how to find the #x#-intercepts for this function:

#x# intercepts have coordinates of #(x,0)#. As such, we set the function #y# equal to #0# and solve for #x# as we did in the other problem you sent me earlier today:

#y=3sin(1/3theta)=0#

#sin(1/3theta)=0#

#1/3theta=0, pi, 2pi, 3pi, 4pi, 5pi, .......#

To solve for #theta#, we multiply both sides of the equation by #3#:

#theta=0, 3pi, 6pi, 9pi, 12pi, 15pi, .....#

If an interval is specified for #theta# then you pick the answers that fall in that interval.

The answer to your question of how to know the values of #(1/3theta)# is:

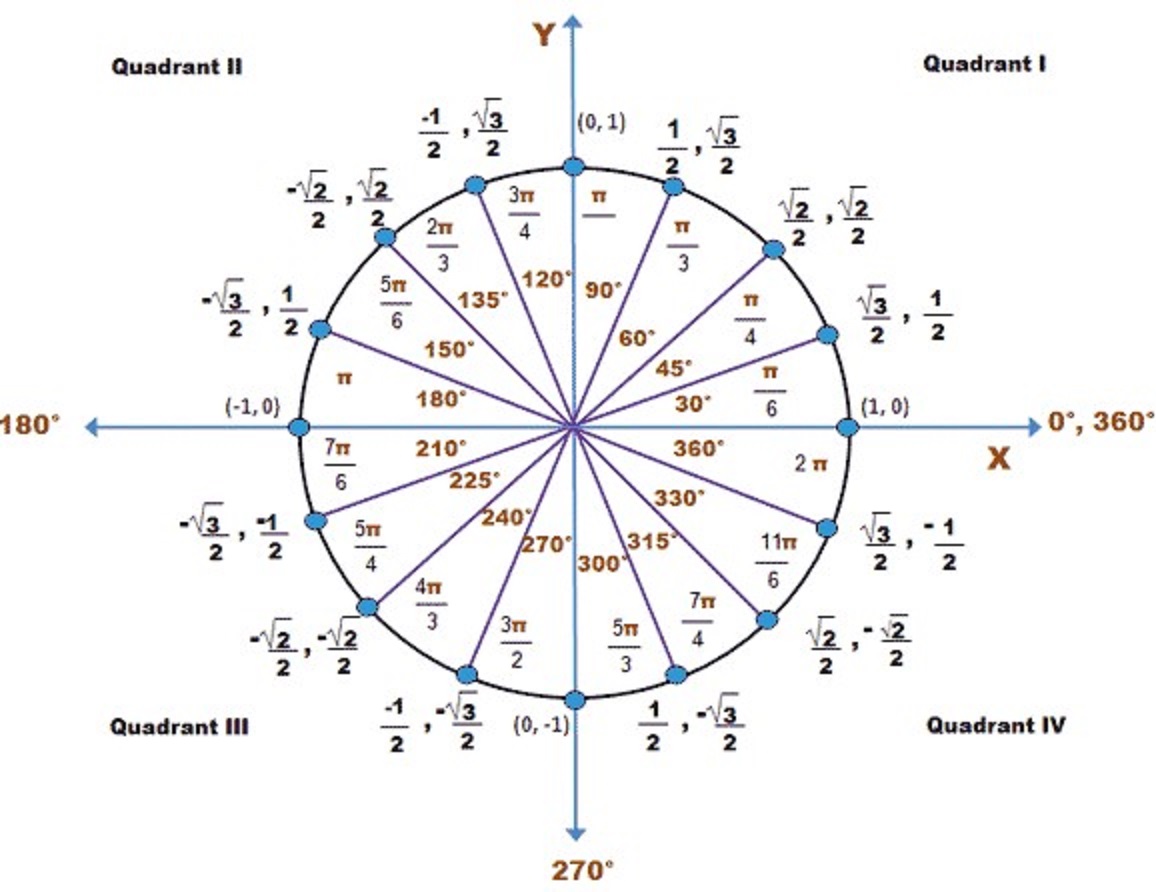
In order to avoid future difficulties in solving trigonometry problems, you need to review and learn the basic concepts that are the foundation of the trig formulas; and be able to remember the values of the sine and cosine of the popular and most often used angles from the unit circle. The unit circle to trigonometry is like the multiplication table to arithmetic and algebra.

Let's look at the image below:

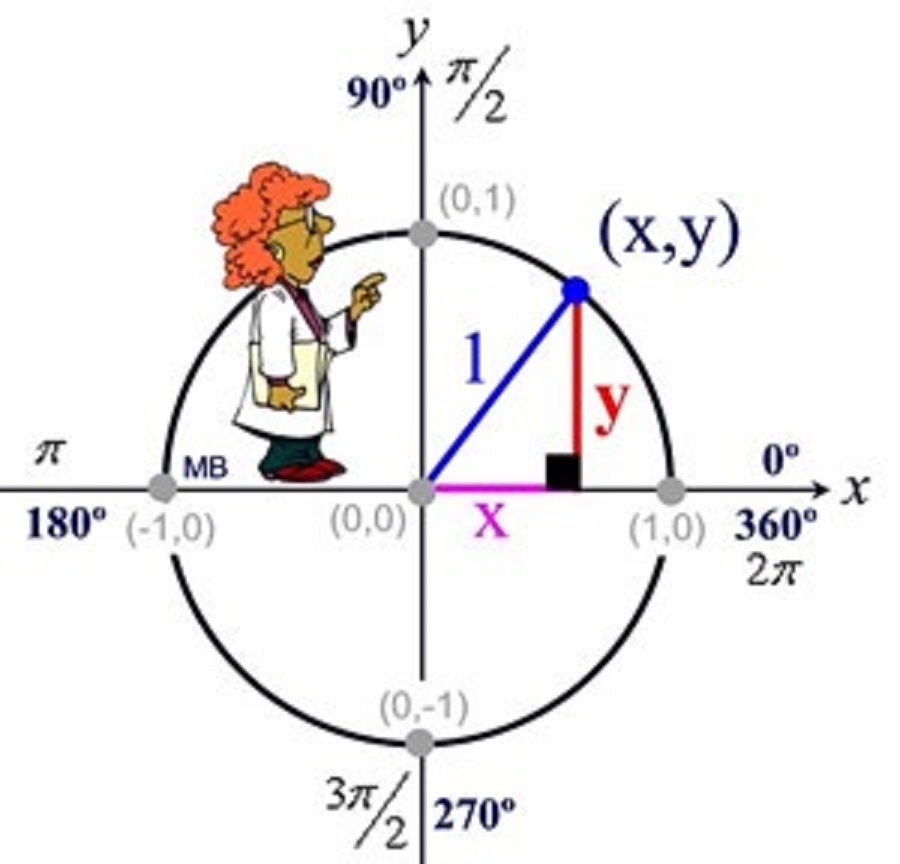
enter image source here

Consider the angle formed by the #x#-axis and the blue line in this unit circle, and call it #theta#. By the way, it is called unit circle because the radius is #1#.

In the right triangle shown, by definition:

#sintheta=("opposite")/("Hypotenuse")=y/1=y#

#costheta=("Adjacent")/("Hypotenuse")=x/1=x#

This means that the coordinates of the blue point on the circle itself shown as #(x,y)# are actually:

#(costheta, sintheta)#

These two values keep changing as the blue point moves around the circle and angle #theta# changes.

As you can see, when the blue point is on the #x#-axis to the right of the origin on the circle, #theta=0# and #y=0, x=1#. This means:

#sin0=0# and #cos0=1#

As the angle opens up and the blue point moves counterclockwise around the circle (positive angle direction), the #sintheta# and #costheta# values change.

When the blue point reaches the #x#-axis to the left of the origin on the circle, #theta=pi# and #sinpi=0#.

As the angle #theta# opens further, the blue point ends up back where we started and #theta=2pi# which is on top of #theta=0#.

This process continues as #theta# increases and we get values of #theta# for which #sintheta=0#, i.e. #3pi, 4pi, 5pi, 6pi, .....#. And that is how we can determine what all the different values of #theta# are if we are given:

#sintheta=0#

The image below shows the unit circle with the values of #sin# and #cos# of popular angles that you need to memorize and be ready to use in solving trig problems. This will happen almost automatically as you solve more problems and look up these values on the unit circle. They will eventually stay in your mind.

enter image source here

Related questions
Impact of this question
1145 views around the world
You can reuse this answer
Creative Commons License