#color(blue)("Preamble")#
For straight line graphs
When they ask 'solve a system of equation' what they are really after is for you to determine any points where they cross. That is; they both have the same x and y values.
For this to happen they either have to have different slopes (gradients) or are on top of each other. In the latter there is an infinite number of shared point.
At least one line that is not straight
The gradient does not come into the consideration
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Answering the question")#
#color(blue)("Both equations to have the same form")#
Given:
#y=1/3x+9" ".....................Equation(1)#
#x-3y=3" "......................Equation(2)#
Consider #Eqn(2) -# A lot of detail so you can see where #color(white)("ddddddddddddddd")#everything comes from (first principles)
Add #3y# to both sides
#color(green)(x-3ycolor(white)(..)=color(white)(..)3 color(white)("dddd")->color(white)("dddd")xcolor(white)("d")ubrace(-3ycolor(red)(+3y))color(white)(..)=color(white)(..)3color(red)(+3y)#
#color(green)(color(white)("dddddddddddddddd")->color(white)("dddd") x color(white)("dd")+0color(white)("ddddd") =color(white)(..)3+3y)#
Subtract 3 from both sides
#color(green)( color(white)("dddddddddddddddd")->color(white)("ddddddddd") x-3color(white)(..)=color(white)(..)3y)#
Divide both sides by 3
#color(green)(color(white)("dddddddddddddddd")->color(white)("dddddddd")1/2x-1color(white)(..)=color(white)(..)y)#
Write as #y=1/3x-1" "............................Equation(2_a)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
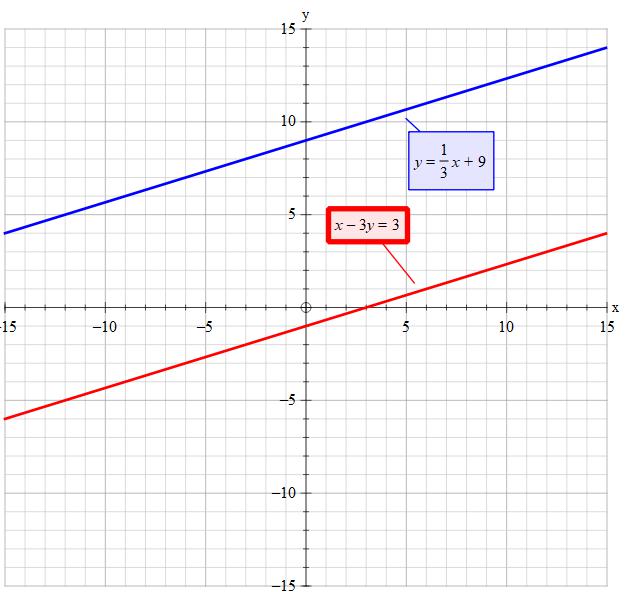
#color(blue)("Comparing equations")#
#y=1/3x+9" ".....................Equation(1)#
#y=1/3x-1" ".....................Equation(2_a)#
#color(brown)("They both have the same slope of "1/3)#
As they have the same slop and cross the y-axis at diferent points they never 'cross'
#color(brown)("There is no solution")#