A triangle has corners at #(3 ,7 )#, #(2 ,9 )#, and #(8 ,4 )#. What is the area of the triangle's circumscribed circle?

2 Answers
Tony B
Mar 7, 2018

area #~~166.216# to 3 decimal places

#color(brown)("The approach by")# https://socratic.org/users/ananda-d #color(brown)("is so much simpler!")#

Explanation:

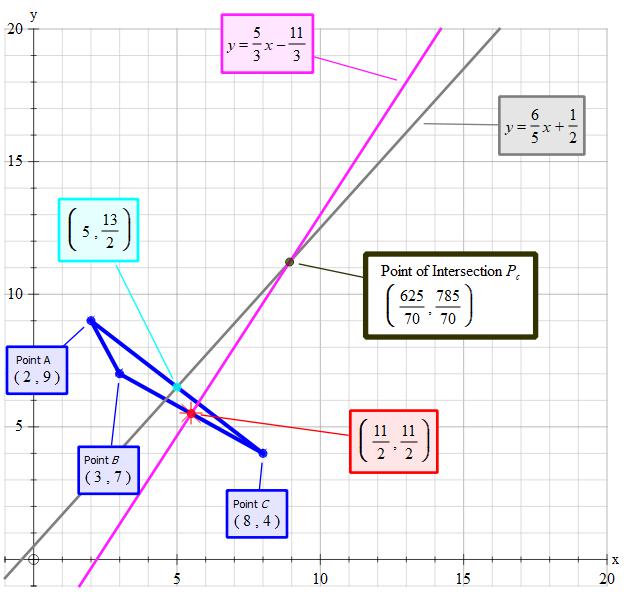
Tony B

Set point 1 as #P_1->(x_1,y_1)=(2,9)#
Set point 2 as #P_2->(x_2,y_2)=(3,7)#
Set point 3 as #P_3->(x_3,y_3)=(8,4)#

The perpendicular from #(P_1+P_3)/2# will coincide with the perpendicular from #(P_2+P_3)/2# at the centre of the circle
(circumcentre).

#color(blue)("Consider mid point "P_1 to P_3=P_4)#

Set mid point as #P_4#

#x_4=(2+8)/2=5 #
#y_4=(9+4)/2=13/2#

#P_4->(x_4,y_4)=(5,13/2)#

#color(blue)("Equation of line perpendicular to "P_1->P_3)#

Set gradient #P_1->P_3=m= (y_3-y_1)/(x_3-x_1)=(4-9)/(8-2)=-5/6#

Perpendicular gradient #=-1/m = +6/5#

So we have #6/5=(y-13/2)/(x-5)#

#6(x-5)=5(y-13/2)#

#6x-30=5y-65/2#

#6x-30+65/2=5y#

#y=6/5x-30/5+65/(5xx2)#

#y=6/5 x+1/2" "......................Equation(1)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

#color(blue)("Consider mid point "P_2 to P_3=P_5)#

#x_5=(3+8)/2=11/2#

#y_5=(7+4)/2=11/2#

#P_5->(x_5,y_5)=(11/2,11/2)#

Set gradient #P_2->P_3=m=(y_3-y_2)/(x_3-x_2) =(4-7)/( 8-3)=-3/5#

Perpendicular gradient# = -1/m=+5/3#

So we have #5/3=(y-11/2)/(x-11/2) #

#5x-55/2=3y-33/2#

#5x-11=3y#

#y=5/3x-11/3" ".....Equation(2)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the centre of the circle")#

Using simultaneous equations for #Eqn(1) and Eqn(2)# we get:

the centre of the circle is at: #P_c->(x_c,y_c)=(625/70, 785/70)#

From this we can derive the radius and hence the area of the circle.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the area of the circle")#

Using Pythagoras on the two points #P_c" and say "P_3#

Let the radius be #r#

#r=sqrt( (x_c-x_3)^2+(y_c-y_3)^2)#

#r=sqrt((625/70-8)^2+(785/70-4)^2)#

#r=sqrt(52.6904...)#

#r~~7.25881......#

area #=pir^2=166.21589...#

area #~~166.216# to 3 decimal places

Ananda Dasgupta
Mar 8, 2018

#~~166.2# (see below)

Explanation:

If you just need the area of the circumscribed circle, the amount of calculations can be reduced a bit by appealing to a simple consequence of the sine law of triangles.

We usually express this law in the form

#a/sin A = b/sin B = c/sin C#

what is often not mentioned is that this common value is, actually the diameter #d# of the circumscribed circle. For a proof, see the figure below

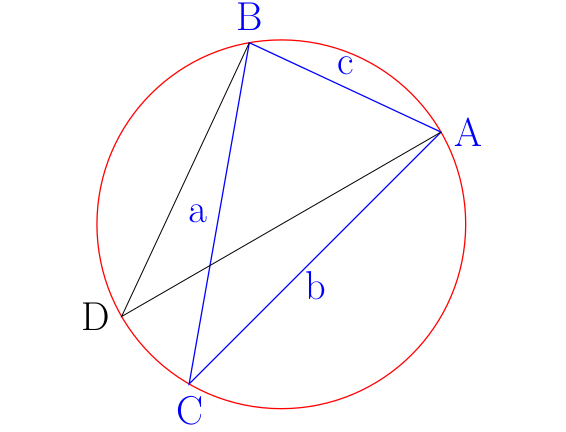
enter image source here

Here ABC is a triangle whose circumscribed circle is drawn in red. AD is a diameter of the circle. Then #/_C = /_BDA# (angles in the same segment of a circle) and #Delta ABD# is right-angled at B (angle in a semicircle). So

#sin/_C = sin/_ADB = {AB}/{AD} = c/d implies d = c/{sin/_C}#

Armed with this result, we first calculate the lengths of the three sides of the given triangle. Let us label the vertices #(3,7)#, #(2,9)#, and #(8,4)# by A, B, and C, respectively, Then

#a^2 = (2-8)^2+(9-4)^2 = 36+25 = 61 implies a = sqrt{61}#
#b^2 = (3-8)^2+(7-4)^2 = 25 + 9= 34 quad implies b = sqrt{34}#
#c^2 = (3-2)^2+(7-9)^2 = 1+4 = 5 qquad quad implies c = sqrt{5}#

We also need one of the angles, say #/_A#. For this we appeal to the cosine law for triangles :

# a^2 = b^2+c^2-2bc cos A implies cos A = {b^2+c^2-a^2}/{2bc} #

With our numbers, we have

#cos A = {34+5-61}/{2sqrt34sqrt5} = -11/sqrt170#

Finally

#d^2 = a^2/{sin^2A} = a^2/(1-cos^2A)= 61/(1-121/170)=61/49 times 170#

So, the area of the circumscribed circle is

# A = pi d^2/4=pi/4 times 61/49 times 170 ~~ 166.2#

Related questions
See all questions in Area of Inscribed Triangle
Impact of this question
1676 views around the world
You can reuse this answer
Creative Commons License