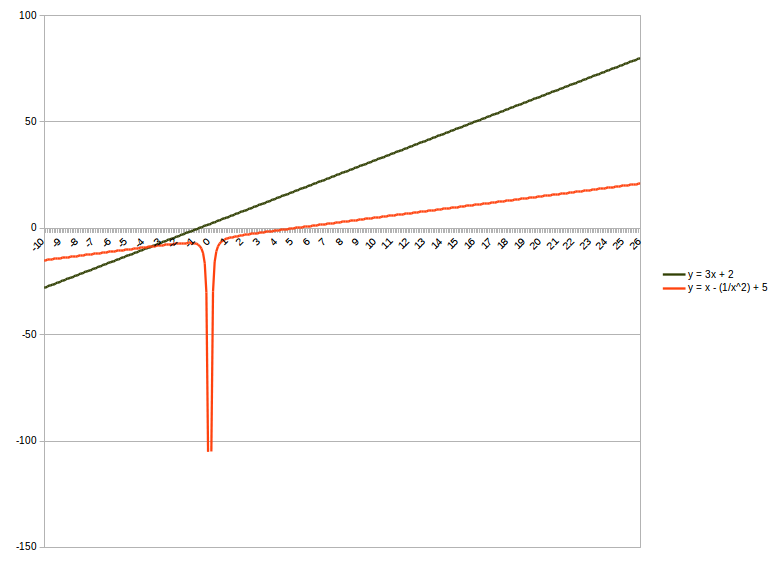
Prove that y=3x+2 has intersection with y=x-(1/x^2)+5 ?
2 Answers
They do intersect. Set them equal to each other with their common variable (x or y).If they have solutions then they intersect.
Explanation:
By setting the two equations equal to each other, you can verify if they intersect by simplifying and solving the equation. If the expression has a solution, there is an intersection and vise versa.
At their intersection, the point (x,y) is a valid input in both equations to make them true. Since x is the same in both equations at this point (or y), we can use this information to set them equal to each other (more accurately, substitute the y or x of one equation with the expression it is equal to in the other equation).
There are solutions for x meaning there are intersections in the two graphs.
A graphical plot shows that there is ONE intersection point near x = -3.5.
Explanation:
It might be proven by finding the solution as a set of linear equations. I could be simpler to just plot the two curves to indicate whether they have an intersection without obtaining the exact numerical solution.
GRAPHICALLY: