How to solve it ?
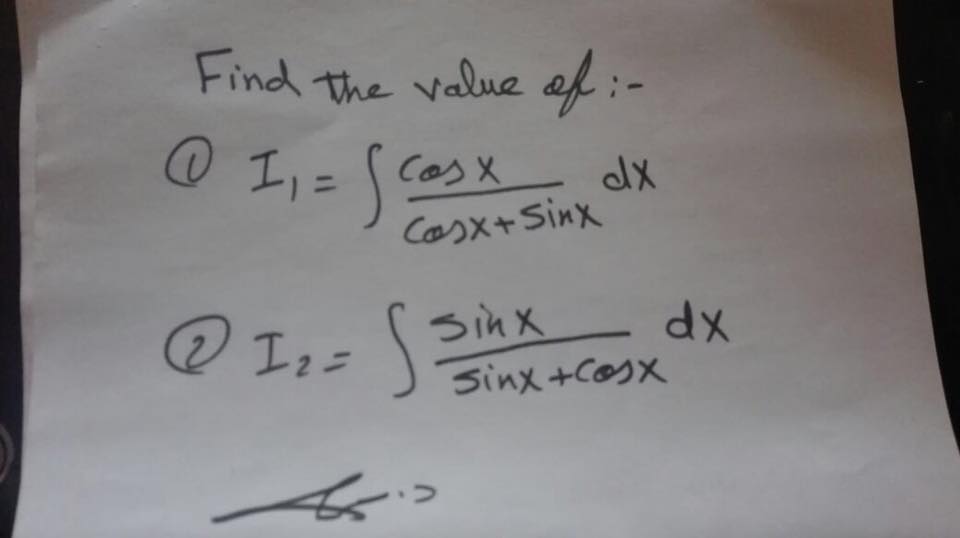
2 Answers
I=1/2(x+ln(cos(x)+sin(x)))+C
Explanation:
We want to solve
I=intcos(x)/(cos(x)+sin(x))dx
We can quite easily find
color(green)(I_1=int(cos(x)+sin(x))/(cos(x)+sin(x))dx andcolor(green)(I_2=int(cos(x)-sin(x))/(cos(x)+sin(x))dx)
So can we find some constants such
I=AI_1+BI_2
Only the denominator have changed, thus we seek
cos(x)=A(cos(x)+sin(x))+B(cos(x)-sin(x))
By letting
1=A+B
color(white)(0=A-Bsscdcfcss)=>A=B=1/2
0=A-B
Therefore
I=1/2int(cos(x)+sin(x))/(cos(x)+sin(x))dx+1/2int(cos(x)-sin(x))/(cos(x)+sin(x))dx
color(white)(I)=1/2intdx+1/2int(1)/(u)du
color(white)(I)=1/2x+1/2ln(u)+C
color(white)(I)=1/2(x+ln(cos(x)+sin(x)))+C
The other can be solve by similar approach
and
Explanation:
Also,
Soving

