How do you integrate?
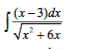
1 Answer
Mar 11, 2018
Use the substitution
Explanation:
Let
#I=int(x-3)/sqrt(x^2+6x)dx#
Complete the square in the square root:
#I=int(x-3)/sqrt((x+3)^2-9)dx#
Apply the substitution
#I=int(3sectheta-6)/(3tantheta)(3secthetatanthetad theta)#
Simplify:
#I=3int(sec^2theta-2sectheta)d theta#
Integrate directly:
#I=3(tantheta-2ln|sectheta+tantheta|)+C#
Rearrange:
#I=3tantheta-6ln|3sectheta+3tantheta|+C#
Reverse the substitution:
#I=sqrt(x^2+6x)-6ln|x+3+sqrt(x^2+6x)|+C#
