Prove that the curves #x = y^2# and #xy = k# cut at right angles if #8k^2 = 1#?

2 Answers
LM
Mar 11, 2018

#-1#

Explanation:

#8k^2 = 1#

#k^2 = 1/8#

#k = sqrt(1/8)#

#x = y^2#, #xy = sqrt(1/8)#

the two curves are

#x = y^2#

and

#x = sqrt(1/8)/y or x = sqrt(1/8)y^-1#

for the curve #x = y^2#, the derivative with respect to #y# is #2y#.

for the curve #x = sqrt(1/8)y^-1#, the derivative with respect to #y# is #-sqrt(1/8)y^-2#.

the point at which the two curves meet is when #y^2 = (sqrt(1/8))/y#.

#y^2 = (sqrt(1/8))/y#.

#y^3 = sqrt(1/8)#

#y = sqrt(1/2)#

since #x = y^2#, #x = 1/2#

the point at which the curves meet is #(1/2, sqrt(1/2))#

when #y = sqrt(1/2)#, #2y = 2sqrt(1/2)#.

the gradient of the tangent to the curve #x = y^2# is #2sqrt(1/2), or 2/(sqrt2)#.

when #y = sqrt(1/2)#, #-sqrt(1/8)y^-2 = -2sqrt(1/8)#.

the gradient of the tangent to the curve #xy = sqrt(1/8)# is #-2sqrt(1/8), or -2/(sqrt8)#.

#(2/sqrt2) * -2/(sqrt*8) = -4/(sqrt16) = -4/4 = -1#

Steve M
Mar 12, 2018

We seek a condition of #k# such that the curves #x=y^2# and #xy=k# "cut at right angles". Mathematically this means the curves should be orthogonal, which in turn means that at all points the tangents to the curves at any given point are perpendicular.

If we examine the family of curves for various values of #k# we get:

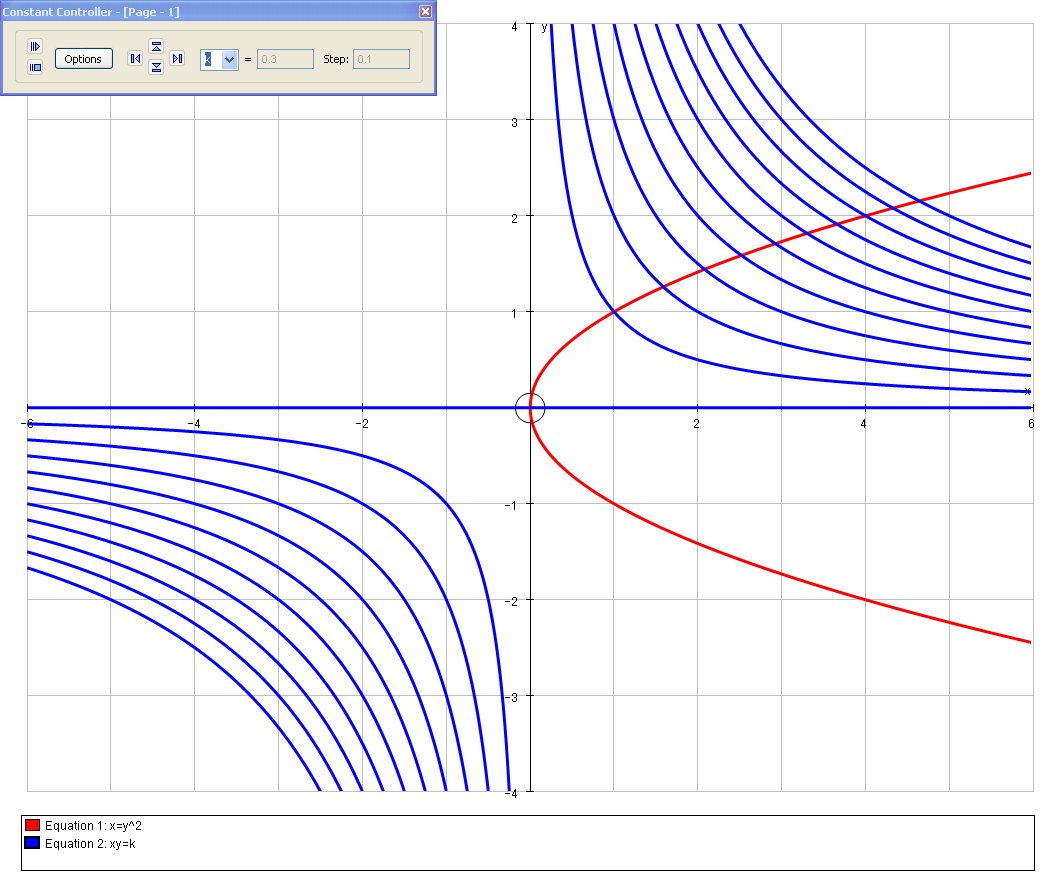Steve M using AutoGraph

We note immediately that we are looking for a single point where the tangent are perpendicular so in general the curves are not orthogonal at all points.

First let us find the single coordinate, #P#, of the point of intersection, which is the simultaneous solution of:

# { (y^2=x, ......[A]), (xy=k, ...... [B]) :} #

Substituting Eq [A] into [B] we get:

# (y^2)y=k => y^3 = k => y = root(3)(k)#

And so we establish the intersection coordinate:

# P(k^(2/3), k^(1/3) )#

We also need the gradients of the tangents at this coordinate. For the first curve:

# y^2=x => 2y dy/dx = 1 #

So the gradient of the tangent, #m_1#, to the first curve at #P# is:

# (2k^(1/3))m_1= 1 => m_1 = 1/(2k^(1/3)) = 1/2k^(-1/3)#

Similarly, for the second curve:

# xy=k => y=k/x => dy/dx = -k/x^2 #

So the gradient of the tangent, #m_2#, to the second curve at #P# is:

# m_2 = -k/(k^(2/3))^2 #
# \ \ \ \ \ = -k^(-1/3) #

If these two tangents are perpendicular then we require that:

# m_1m_2 = -1#

# :. (1/2k^(-1/3)) \ (-k^(-1/3)) = -1 #

# :. k^(-2/3) = 2 #

# :. (k^(-2/3))^(3/2) = 2^(3/2) #

# :. k^(-1) = 2^(3/2) #

# :. (1/k)^2 = 2^3 #

# :. 1/k^2 = 8 #

Leading to the given result:

# 8k^2=1 \ \ \ # QED

And with this value of #k#

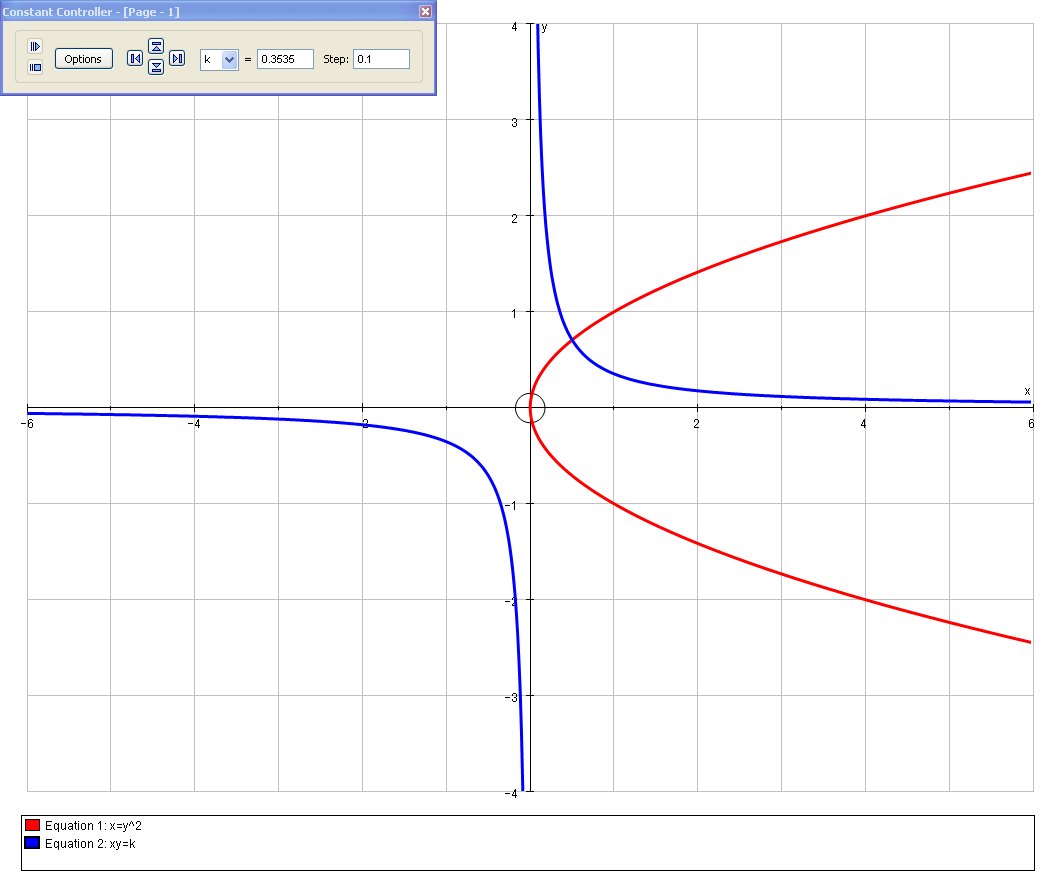Steve M using AutoGraph

Related questions
Impact of this question
13778 views around the world
You can reuse this answer
Creative Commons License