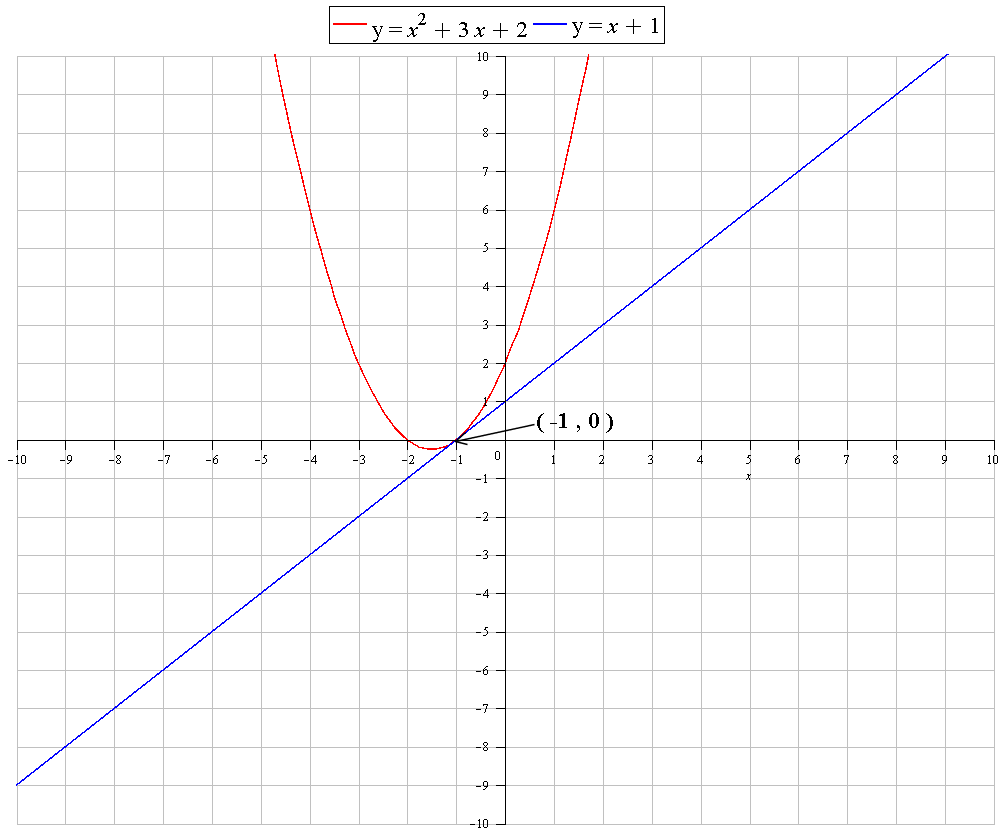
What is the equation of the tangent line of #f(x) =x^2+3x+2# at #x=-1#?
1 Answer
Mar 13, 2018
Explanation:
To find the equation of the tangent line at
Differentiating
Note that
i.e
Plugging in
We now need a corresponding value of
Using
Using point slope form of a line, where
GRAPH: