Question

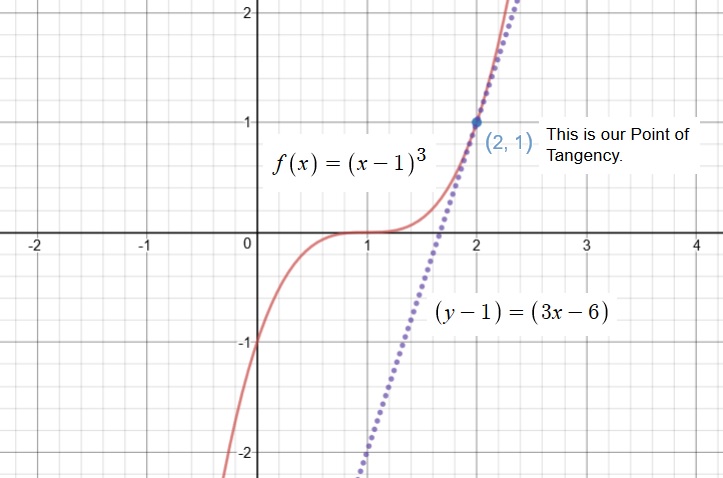
What is the equation of the tangent line of `f(x)=(x-1)^3` at `x=2`?

Answer 1

This is our final answer in Point-Slope Form.

`color(blue)(y-1=3x-6`

Explanation:

The tangent line is the line that touches the curve of the given function at one point exactly.

To solve our given problem, we must find the equation of the tangent line of the function `color(red)(f(x)=(x-1)^3`, at `color(green)(x=2`.

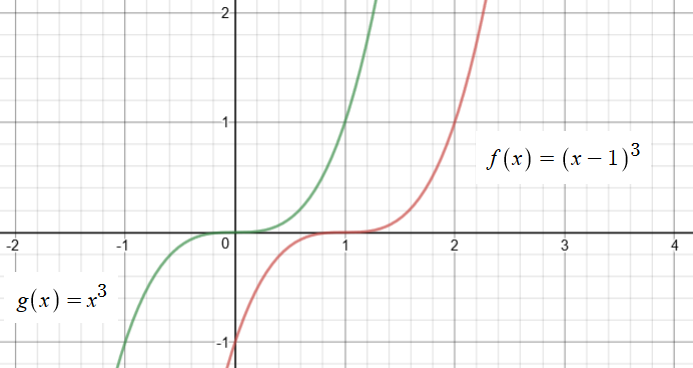
To understand the behavior of the given function, let us examine the graphs of the original function given and also it's base function.

Step 1:

Take the first derivative of the function given.

We have,

`color(blue)(y = f(x) = (x-1)^3`

`d/dx(x-1)^3`

We will use the Power Rule to differentiate.

`rArr 3(x-1)^2.d/(dx)(x-1)`

`rArr 3(d/(dx)(x)+d/(dx)(-1))(x-1)^2`

`rArr 3(1+0)(x-1)^2`

`rArr 3(x-1)^2`

`:. d/(dx)(x-1)^3 = 3(x-1)^2`

Step 2:

Get the `color(red)(x` value given in the problem.

Substitute in the first derivative we have just found.

Derivative gives the Slope of the tangent line to a specific function.

`:. f'(x) = 3(x-1)^2`

`rArr f'(2) = 3(2-1)^2`

`rArr 3(1)^2`

`rArr 3`

`color(blue)( :. f'(2) = 3`

This will be the Slope value (m) we will use later.

Step 3:

In this step, we must find the y-coordinate value.

We use the original function given in the problem and substitute the value of `x=2`, to find `y`.

`y = (x-1)^3`, given `x=2`.

`:.y=(2-1)^3`

`rArr y = 1^3`

`:. y = 1`

Hence, we have `(2,1)` for `color(red)((x_1, y_1)`.

We will use this value in our next step.

Step 4:

We must substitute the value of `color(red)((x_1, y_1)` into the Point-Slope Formula for a line.

Point-Slope Formula is gven by:

`color(blue)(y-y_1=m(x-x_1)`, where `color(blue)(m` is the Slope.

`y-1=3(x-2)`

`y-1=3x-6` is our answer in the Point-Slope Form.

Please examine the image of the graph below: