How do I plot the energy eigenvalues and wave function solutions of a delta function double potential well with #V(chi) = -alpha(delta(chi+L)+delta(chi-L))#?
1 Answer
Well, here it is... Here is the Excel sheet I made while doing this. Also, here are the even solution graphs.
This, by the way, results in a wave function solution that resembles the hydrogen molecule, except with internuclear distance
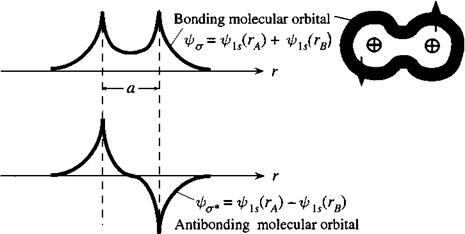
This is the case because
DISCLAIMER: VERY LONG ANSWER!
Here's the scenario (just change
We set up the wave function for a tunnelling free-particle. Call the regions
#psi_I = Ae^(-kchi) + Be^(kchi)#
#psi_(II) = Ce^(-kchi) + De^(kchi)#
#psi_(III) = Fe^(-kchi) + Ge^(kchi)# where
#k = sqrt(-(2mE)/ℏ^2)# , since#E < 0# for bound states.
Since the wave function must vanish at
#C = D# for even solutions and#C = -D# for odd solutions.#G = B# for even solutions and#G = -B# for odd solutions.
This simplifies down to even solutions being:
#psi_"even" = {(Be^(kchi),-oo < chi < -L),(C(e^(-kchi) + e^(kchi)),-L < chi < L),(Be^(-kchi),L < chi < oo):} #
and odd solutions being:
#psi_"odd" = {(-Be^(kchi),-oo < chi < -L),(C(e^(-kchi) - e^(kchi)),-L < chi < L),(Be^(-kchi),L < chi < oo):} #
EVEN SOLUTION
Continuity at
#Be^(-kL) = C(e^(kL) + e^(-kL))#
#=> B = C(e^(2kL) + 1)#
Next, consider the Schrodinger equation at just
#-ℏ^2/(2m) (d^2psi)/(dchi^2) - alphadelta(chi+L)psi = Epsi#
Integration near
#-ℏ^2/(2m) lim_(epsilon->0) int_(-L-epsilon)^(-L + epsilon) (d^2psi)/(dchi^2) dchi - alpha lim_(epsilon->0) int_(-L-epsilon)^(-L+epsilon) delta(chi+L)psidchi = lim_(epsilon -> 0) Eint_(-L-epsilon)^(-L+epsilon) psidchi#
Denote
#-ℏ^2/(2m) int_(-L^(-))^(-L^(+)) (d^2psi)/(dchi^2) dchi - alpha int_(-L^(-))^(-L^(+)) delta(chi+L)psidchi = 0#
Evaluating the integrals requires examination of the left and right sides of the discontinuous derivative.
#-ℏ^2/(2m) (Delta (dpsi(-L))/(dchi)) = alpha psi(-L^(pm))#
Now evaluate the
#-ℏ^2/(2m) (-kCe^(kL) + kCe^(-kL) - kBe^(-kL)) = alpha Be^(-kL)#
#C(-e^(kL) + e^(-kL)) - Be^(-kL) = -(2malpha)/(ℏ^2k) Be^(-kL)#
Multiply through by
#C(-e^(2kL) + 1) = B - (2malpha)/(ℏ^2k) B#
#C(e^(2kL) - 1) = B((2malpha)/(ℏ^2k) - 1)#
Seeing as we have an expression for
#cancelC(e^(2kL) - 1) = cancelC(e^(2kL) + 1)((2malpha)/(ℏ^2k) - 1)#
#e^(2kL) - 1 = (2malpha)/(ℏ^2k)e^(2kL) - e^(2kL) + (2malpha)/(ℏ^2k) - 1#
#e^(2kL) = ((2malpha)/(ℏ^2k) - 1)e^(2kL) + (2malpha)/(ℏ^2k)#
#1 = (2malpha)/(ℏ^2k) - 1 + (2malpha)/(ℏ^2k)e^(-2kL)#
#cancel2(1 - (malpha)/(ℏ^2k)) = cancel2[(malpha)/(ℏ^2k)e^(-2kL)]#
#color(blue)(e^(-2kL) = (ℏ^2k)/(malpha) - 1)#
Let
Clearly, there will always be an intersection (always at least one bound state) as long as
The x-intercept turns out to be
So the approximate even solution energy for
#1.27846 ~~ 2kL#
#=> k^2 ~~ 0.40861/L^2 = -(2mE)/(ℏ^2)#
#=> color(blue)(E ~~ -(0.20431ℏ^2)/(mL^2))#
If we take the limit as
ODD SOLUTION
Continuity at
#Be^(-kL) = C(e^(-kL) - e^(kL))#
#=> B = -C(e^(2kL) - 1)#
As before, consider the Schrodinger equation at just
#-ℏ^2/(2m) (d^2psi)/(dchi^2) - alphadelta(chi-L)psi = Epsi#
Integration near
#-ℏ^2/(2m) int_(L^(-))^(L^(+)) (d^2psi)/(dchi^2) dchi - alpha int_(L^(-))^(L^(+)) delta(chi-L)psi = 0#
As before, we now get:
#-ℏ^2/(2m) (Delta (dpsi(L))/(dchi)) = alpha psi(L^(pm))#
Now evaluate the
#-ℏ^2/(2m) (-kBe^(-kL) + kCe^(-kL) + kCe^(kL)) = alpha Be^(-kL)#
#(ℏ^2k)/(2malpha) (Be^(-kL) - Ce^(-kL) - Ce^(kL)) = Be^(-kL)#
Again multiply through by
#(ℏ^2k)/(2malpha) (B - C - Ce^(2kL)) = B#
#(ℏ^2k)/(2malpha) (-C - Ce^(2kL)) = B(1 - (ℏ^2k)/(2malpha))#
#(ℏ^2k)/(2malpha) C(1 + e^(2kL)) = B((ℏ^2k)/(2malpha) - 1)#
#C(1 + e^(2kL)) = B(1 - (2malpha)/(ℏ^2k))#
Now plug in
#cancelC(1 + e^(2kL)) = cancelC(1 - e^(2kL))(1 - (2malpha)/(ℏ^2k))#
#1 + e^(2kL) = 1 - (2malpha)/(ℏ^2k) - e^(2kL) + e^(2kL)(2malpha)/(ℏ^2k)#
#cancel2e^(2kL) - e^(2kL)(cancel2malpha)/(ℏ^2k) = - (cancel2malpha)/(ℏ^2k)#
#1 - (malpha)/(ℏ^2k) = - (malpha)/(ℏ^2k)e^(-2kL)#
#color(blue)(e^(-2kL) = 1 - (ℏ^2k)/(malpha))#
Now we again let
The y-intercept turns out to be
HOW DO THE WAVE FUNCTIONS LOOK?
We'll get two bound states if
The even solution energy for
#2.21772 ~~ 2kL#
#=> k^2 ~~ 1.22957/L^2 = -(2mE)/(ℏ^2)#
#=> color(blue)(E ~~ -(0.61479ℏ^2)/(mL^2))#
In this case we can then get
#k = sqrt(-(2m)/ℏ^2 cdot -(0.61479ℏ^2)/(mL^2))#
#= sqrt(2 cdot (0.61479)/(L^2)) = 1.10886/L# where I simply chose
#B = 1# and#C = 0.0981705# to match#psi# at the boundaries.
#=> psi_(I) = Be^(1.10886x//L)#
#=> psi_(II) = C(e^(-1.10886x//L) + e^(1.10886x//L))#
#=> psi_(III) = Be^(-1.10886x//L)#
This results in (the
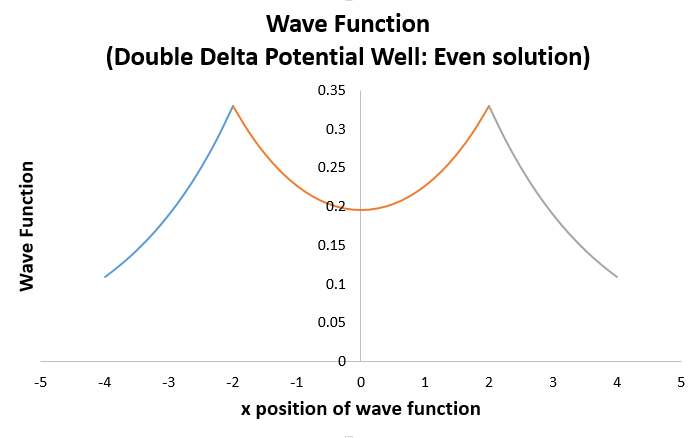
This looks remarkably like the hydrogen bonding molecular orbital wave function plot!
Then, we get
#1.59362 ~~ 2kL#
#=> k^2 ~~ 0.63491/L^2 = -(2mE)/(ℏ^2)#
#=> color(blue)(E ~~ -(0.31745ℏ^2)/(mL^2))#
The other bound state (odd solution) has:
#k = sqrt(-(2m)/ℏ^2 cdot -(0.31745ℏ^2)/(mL^2))#
#= sqrt(2 cdot (0.31745)/(L^2)) = 0.79681/L#
#=> psi_(I) = -Be^(0.79681x//L)#
#=> psi_(II) = C(e^(-0.79681x//L) - e^(0.79681x//L))#
#=> psi_(III) = Be^(-0.79681x//L)#
Here I just chose
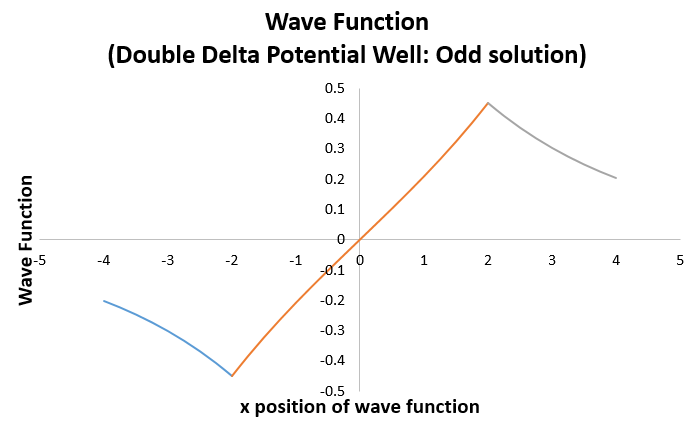
which looks like the hydrogen antibonding molecular orbital wave function plot!
(Again, the
What if we choose
If
Hence, we discard the odd solution and only have an even solution:
#0.73884 ~~ 2kL#
#=> k^2 ~~ 0.13647/L^2 = -(2mE)/(ℏ^2)#
#=> color(blue)(E ~~ -(0.06824ℏ^2)/(mL^2))#
With this scenario,
#k = sqrt(-(2m)/ℏ^2 cdot -(0.06824ℏ^2)/(mL^2))#
#= sqrt(2 cdot (0.06824)/(L^2)) = 0.36943/L#
You can plug it back in if you wish, but I'm not going to plot this one, because it's unphysical; since this entire problem can be used to model something not unlike

