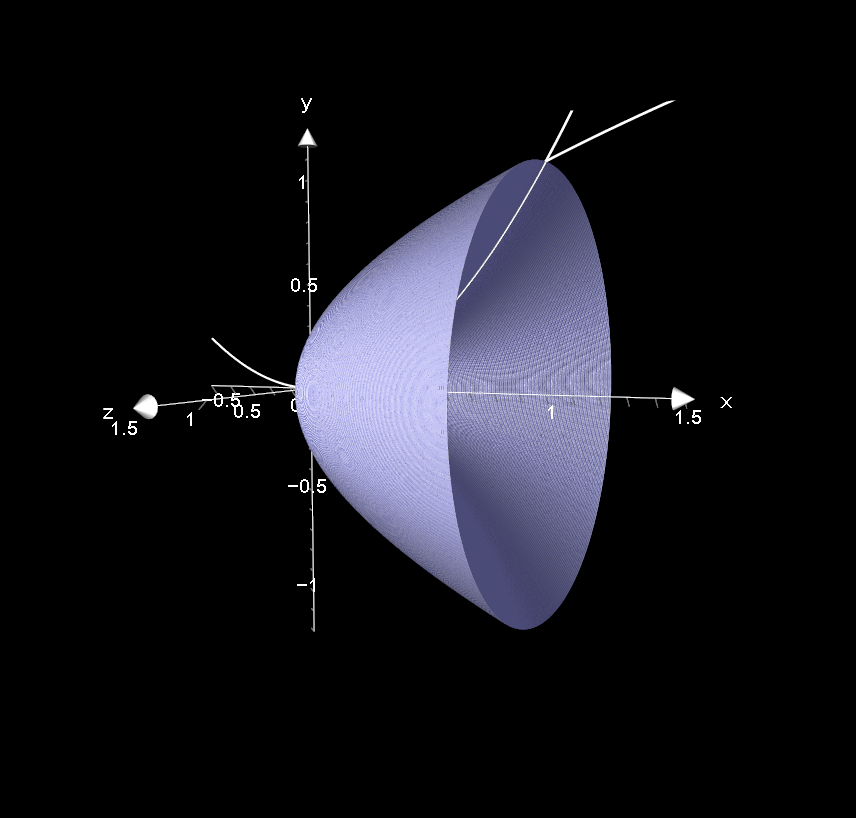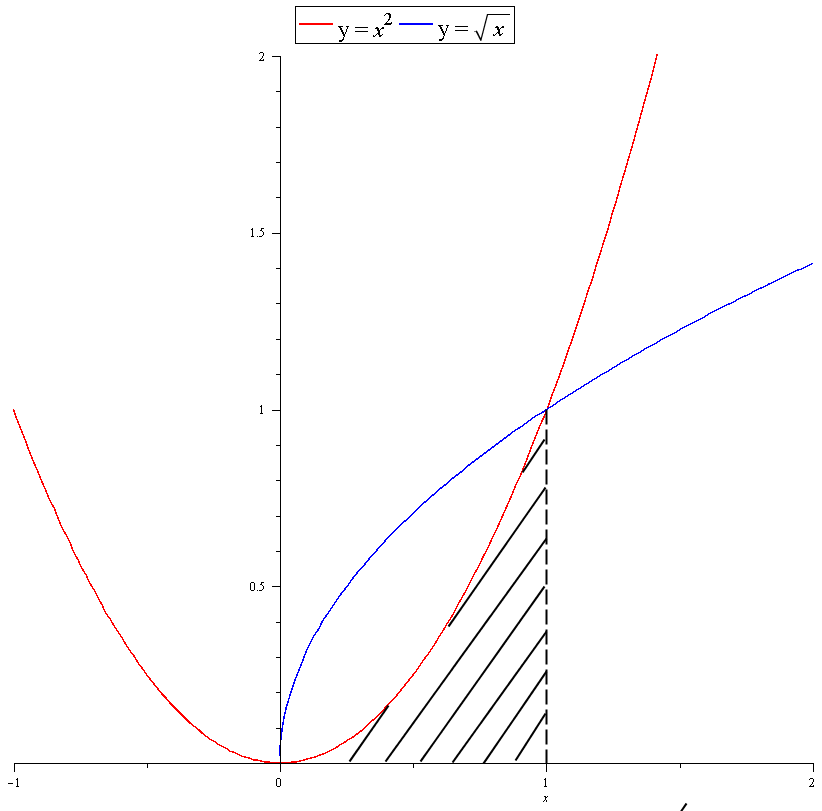
From the graph we can see that the volume we seek is between the two functions. In order to find this, we must find the volume of revolution of #f(x)=sqrt(x)# and subtract the volume of revolution of #f(x)=x^2#. This is shown as the shaded area.
First we need to find the upper and lower bounds. We know the lower bound is #0# since #f(x)=sqrt(x)# is undefined for #x<0#. The upper bound is where the functions intersect:
#:.#
#x^2=sqrt(x)#
#x^2/x^(1/2)=1#
#x^(3/2)=1#
Squaring:
#x^3=1#
#x=root(3)(1)=1#
Volume of #bb(f(x)=sqrt(x))#:
#pi int_(0)^(1)(x^(1/2))=pi[2/3x^(3/2)]_(0)^(1)#
#=pi{[2/3x^(3/2)]^(1)-[2/3x^(3/2)]_(0)}#
Plugging in upper and lower bounds:
#=pi{[2/3(1)^(3/2)]^(1)-[2/3(0)^(3/2)]_(0)}=(2pi)/3# cubic units
Volume of #bb(f(x)=x^2)#
#pi int_(0)^(1)(x^2)=pi[1/3x^3]_(0)^(1)#
#=pi{[[1/3x^3]^(1)-[1/3x^3]_(0)}#
Plugging in upper and lower bounds:
#=pi{[[1/3(1)^3]^(1)-[1/3(0)^3]_(0)}=pi/3# cubic units.
Required volume is:
#(2pi)/3-pi/3=##color(blue)(pi/3 "cubic units.")#
Volume of revolution: