Question

A soda can is to hold 12 fluid ounces. Find the dimensions that will minimize the amount of material used in its construction, assuming the thickness of the material is uniform?

I am Canadian so I don't know imperial measurements by the way !

Answer 1

`r=root(3)(341/(2pi))color(white)(88)` and `color(white)(88)h=341/(pi(root(3)(341/(2pi)))^2`

Explanation:

I have converted fluid ounces to cubic centimetres.

`12 "flz"= 341 "cm"^3` (1 d.p.)

We need the can to have a volume of `341cm^3` and a minimum surface area.

If the can has a radius `bbr` and height `bbh` Then the surface area is given by:

`bb(S=2pir^2+2pirh)`

We can't differentiate this expression in the given form, because it contains two variables `bbr` and `bbh`

But the volume given by:

`bb(V=pir^2h)`

needs to be `341cm^3`

`:.`

`pir^2h=341`

We can now find `bbh` in terms of the radius `bbr`:

`h=341/(pir^2)`

Substituting this into the surface area formula:

`S=2pir^2+2pir(341/(pir^2))`

Simplifying:

`S=2pir^2+2pir(341/(pir^2))=2pir^2+(pir682)/(pir^2)`

`->S=2pir^2+682/r`

Since we need to find the change in surface area as the radius changes, we need to differentiate this in respect of `bbr`:

`(dS)/(dr)(2pir^2+682/r)=4pir-682/r^2`

Now we know that local maximum and minimum points have a gradient of zero. These therefore can be identified using our first derivative and equating this to zero.

`:.`

`4pir-682/r^2=0`

Solving for `bbr`

`r^3=341/(2pi)`

`r=root(3)(341/(2pi))`

`h=341/(pi(root(3)(341/(2pi)))^2)color(white)(88888)` ( From above )

We know that if the second derivative is `>0` for our value of `bbr` then this is a minimum value.

`(d^2S)/(dr^2)=4pi+(2(682))/r^3`

Plugging in our value for `bbr`

`4pi+(2(682))/(root(3)(341/(2pi)))^3=4pi+(2(682))/(341/(2pi))`

This is greater than zero, so `r=root(3)(341/(2pi))` and `h=341/(pi(root(3)(341/(2pi)))^2`

So a can with our given radius an height will have a minimum surface area.

Note: Dimensions will be in cm, since we converted volume into these units. `bbr` and `bbh` can be approximated in necessary, but I will leave them in their exact form.

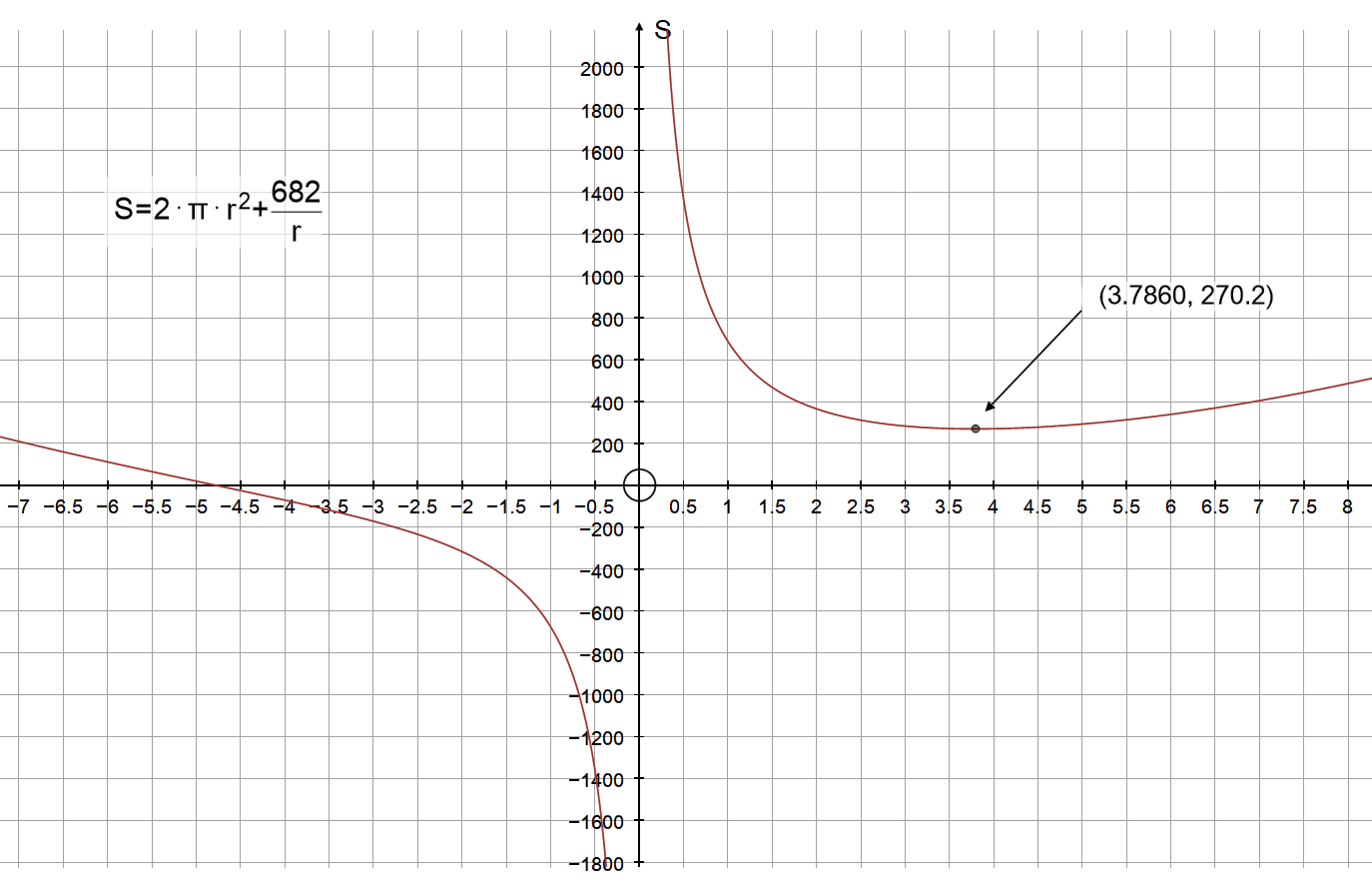
Below is the graph of surface area in terms of radius and height. If you approximate the found values of `bbr` you will see that this is the minimum value, and this give a surface area of `~~270.2cm^2`.

Graph of `S=2pir^2+682/r`