Question

How to plot the transmission coefficient as a function of `E//V_0`?

Answer 1

Here is the Excel sheet I made while doing this.

Here we follow what is readily found in McQuarrie & Simon (pp. 142-143). We found that:

`T = {([1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r))]^(-1),0 < r < 1),([1 + [sin^2[v_0^(1//2)(r - 1)^(1//2)]]/(4r(r - 1))]^(-1),r >= 1):}`

where:

• `T` is the transmission coefficient (i.e. the fraction of particles that tunnel).
• `r = E/V_0 = epsilon/v_0` is the ratio of the particle energy to the barrier height.
• `v_0 = (2ma^2V_0)/ℏ^2` is a unitless variable for the height of the barrier.
• `epsilon = (2ma^2E)/ℏ^2` is a unitless variable for the energy of the particle.

and because I thought it would be interesting, besides `v_0 = 10`, I also graphed `v_0 = 10, 20, 40`:

It is rather interesting that the higher the barrier gets, the more values of `E` there are that allow for `100%` transmission. Here we have:

`ul(V_0" "" "" "" "" "E//V_0" "" "" "%T" ")`
`10ℏ^2//2ma^2" "color(white)(.)1.99" "" "" "" "100%`
`" "" "" "" "" "" "4.95`

`20ℏ^2//2ma^2" "color(white)(.)1.49" "" "" "" "`
`" "" "" "" "" "" "2.97`

`40ℏ^2//2ma^2" "color(white)(.)1.25" "" "" "" "`
`" "" "" "" "" "" "1.99`
`" "" "" "" "" "" "3.22`
`" "" "" "" "" "" "4.95`

It just so happens that at the classical limit, we have

`lim_(V_0 -> oo) T = 100%` for `E > V_0`,

with a rigid cutoff at `E = V_0`. That's just what we expect. Classically, particles can't tunnel unless they have enough energy. Here is the same graph at `v_0 = 10^6`:

---

DISCLAIMER: LONG AND RIGOROUS DERIVATION!

The potential is set up as:

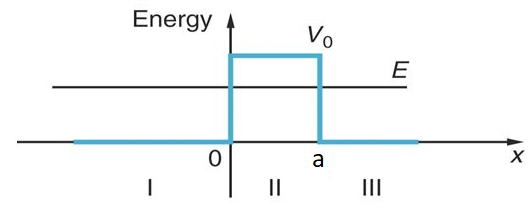
`V(x) = {(0, x < 0),(V_0, 0 < x < a),(0, x > a):}`

We of course set `E < V_0` to allow tunnelling, and the eigenfunctions are:

`psi_I(x) = Ae^(ikx) + Be^(-ikx), " "x < 0`
`psi_(II)(x) = Ce^(k'x) + De^(-k'x), " "0 < x < a`
`psi_(III)(x) = Fe^(ikx) + Ge^(-ikx), " "x > a`

where `k = sqrt((2mE)/ℏ^2)` and `k' = sqrt((2m(V_0 - E))/ℏ^2)`.

If we restrict the particle to only come in from the left, `G = 0`. Then, the transmission coefficient is given by

`T = (|F|^2)/(|A|^2)`

The continuity conditions are:

`ul(psi_I(0) = psi_(II)(0))`:
`A + B = C + D` `" "" "" "" "" "" "bb((1))`

`ul((dpsi_I(0))/(dx) = (dpsi_(II)(0))/(dx))`:
`ik(A - B) = k'(C - D)` `" "" "" "bb((2))`

`ul(psi_(II)(a) = psi_(III)(a))`:
`Ce^(k'a) + De^(-k'a) = Fe^(ika)` `" "" "" "bb((3))`

`ul((dpsi_(II)(a))/(dx) = (dpsi_(III)(a))/(dx))`:
`k'Ce^(k'a) - k'De^(-k'a) = ikFe^(ika)` `" "bb((4))`

Now, we take `ik(1) + (2)` to get:

`color(green)(2ikA = (ik + k')C + (ik - k')D)`

Then, take `k'(3) + (4)` to get `C` in terms of `F`:

`2k'Ce^(k'a) = (k' + ik)Fe^(ika)`

`color(green)(C = ((k' + ik)/(2k'))Fe^(ika)e^(-k'a))`

and take `k'(3) - (4)` to get `D` in terms of `F`:

`2k'De^(-k'a) = (k' - ik)Fe^(ika)`

`color(green)(D = ((k' - ik)/(2k'))Fe^(ika)e^(k'a))`

Plug it back into the first result to get:

`2ikA = (ik + k')((k' + ik)/(2k'))Fe^(ika)e^(-k'a) + (ik - k')((k' - ik)/(2k'))Fe^(ika)e^(k'a)`

`= [(ik - k')(k' - ik)e^(k'a) + (ik + k')(k' + ik)e^(-k'a)] (Fe^(ika))/(2k')`

`= [(k^2 - k'^2 + 2ikk')e^(k'a) + (k'^2 - k^2 + 2ikk')e^(-k'a)] (Fe^(ika))/(2k')`

`= [(k^2 - k'^2)(e^(k'a) - e^(-k'a)) + 2ikk'(e^(k'a) + e^(-k'a))] (Fe^(ika))/(2k')`

Now, we use the identities `2sinh(x) = e^x - e^(-x)` and `2cosh(x) = e^x + e^(-x)` to get:

`2ikA = [2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)] (Fe^(ika))/(2k')`

Solve for `F/A` to get:

`F/A = (2ik)/{[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]e^(ika)/(2k')}`

`= (4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]`

Using the definition of `T`,

`T -= (F^"*"F)/(A^"*"A) = [(4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]]^"*" [(4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]]`

`= (4k^2k'^2)/((k^2 - k'^2)^2sinh^2(k'a) + 4k^2k'^2cosh^2(k'a))`

Next, use the identity that `cosh^2(x) = 1 + sinh^2(x)` to get:

`T = (4k^2k'^2)/((k^2 - k'^2)^2sinh^2(k'a) + 4k^2k'^2 + 4k^2k'^2sinh^2(k'a))`

`= (4)/(4 + (k^2 - k'^2)^2/(k^2k'^2)sinh^2(k'a) + 4sinh^2(k'a))`

`= (4)/(4 + (k^4 - 2k^2k'^2 + k'^4)/(k^2k'^2)sinh^2(k'a) + (4k^2k'^2)/(k^2k'^2) sinh^2(k'a))`

`= (4)/(4 + (k^4 + 2k^2k'^2 + k'^4)/(k^2k'^2)sinh^2(k'a))`

`= (4)/(4 + (k^2 + k'^2)^2/(k^2k'^2)sinh^2(k'a))`

Then, insert `k` and `k'` in terms of `E` and `V_0` to get:

`T = (4)/(4 + ((2mV_0)/ℏ^2)^2/(((2m)/ℏ^2)^2 E(V_0 - E))sinh^2(sqrt((2ma^2(V_0 - E))/ℏ^2)))`

`= 4/(4 + (V_0^2)/(E(V_0 - E))sinh^2(sqrt((2ma^2(V_0 - E))/ℏ^2)))`

Now, let the unitless quantities `v_0 = (2ma^2V_0)/ℏ^2`, and `epsilon = (2ma^2E)/ℏ^2`. This means that:

`V_0 = (ℏ^2v_0)/(2ma^2)`, `" "E = (ℏ^2epsilon)/(2ma^2)`

and we then rewrite `T` as:

`T = 4/(4 + (((ℏ^2)/(2ma^2))^2v_0^2)/((ℏ^2epsilon)/(2ma^2)((ℏ^2v_0)/(2ma^2) - (ℏ^2epsilon)/(2ma^2)))sinh^2(sqrt(v_0 - epsilon)))`

`= 4/(4 + (cancel(((ℏ^2)/(2ma^2))^2)v_0^2)/(cancel(((ℏ^2)/(2ma^2))^2) epsilon(v_0 - epsilon))sinh^2(sqrt(v_0 - epsilon)))`

`= 1/(1 + (v_0^2)/(4epsilon(v_0 - epsilon))sinh^2(sqrt(v_0 - epsilon)))`

Finally, let `r = E/V_0 = epsilon/v_0` so that we can graph `T` vs. `E//V_0 -= r`:

`T = 1/(1 + cancel(v_0^2)/((4epsilon)/v_0 cancel(v_0^2)(1 - r))sinh^2(sqrt(v_0(1 - r))))`

`= barul|" "1/(1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r)))" "|`

Now, when we plot this, if we want `r > 1`, i.e. `E > V_0`, then we would need to use the identity `sinh(ix) = isinx`. So, we separate our result into two segments:

`color(blue)(T = {([1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r))]^(-1),0 < r < 1),([1 + [sin^2[v_0^(1//2)(r - 1)^(1//2)]]/(4r(r - 1))]^(-1),r >= 1):})`

Let's choose `v_0 = 10`. Then this produces the following graph: