If the arithmetic mean of two numbers, a and b, a > b > 0, is five times their geometric mean, then what is (a+b)/(a-b) equal to?
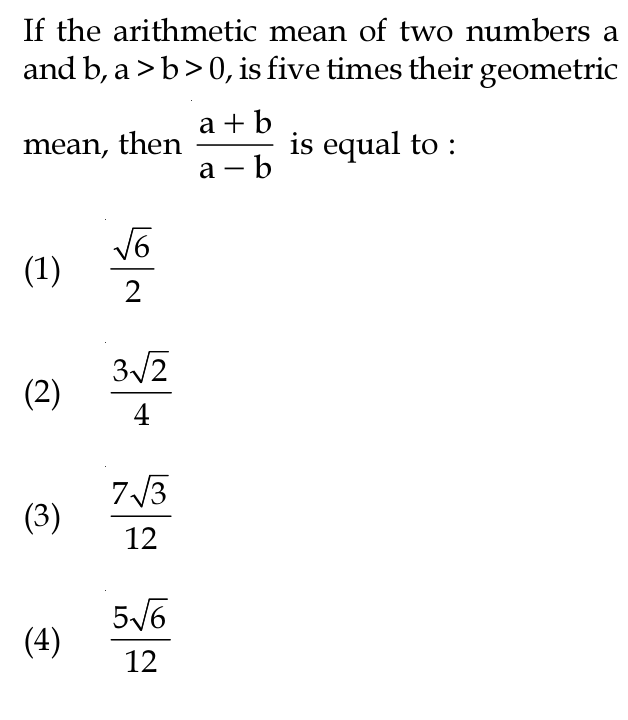
1 Answer
Mar 18, 2018
Explanation:
From the information we are given:
1/2(a+b) = 5sqrt(ab)
Multiply both sides by
a+b = 10sqrt(ab)
Square both sides to get:
(a+b)^2 = a^2+2ab+b^2 = 100ab
Subtract
(a-b)^2 = a^2-2ab+b^2 = 96ab
So:
((a+b)/(a-b))^2 = (100ab)/(96ab) = 25/24 = (5^2 * 6)/12^2 = ((5sqrt(6))/12)^2
So since
(a+b)/(a-b) = (5sqrt(6))/12

