Can you please make the MO diagrams for these ?

1 Answer
TRANS-BUTADIENE
If you follow the extensive process shown here that goes through Huckel MO theory, you'll get:
E_1 = alpha + 1.62beta
E_2 = alpha + 0.62beta
E_3 = alpha - 0.62beta
E_4 = alpha - 1.62beta where
alpha is the nonbonding reference energy, andbeta < 0 is the offset from the nonbonding energy.
So,
Here, the first antibonding orbital (corresponding to
psi_3 = 0.60p_1 - 0.37p_2 - 0.37p_3 + 0.60p_4
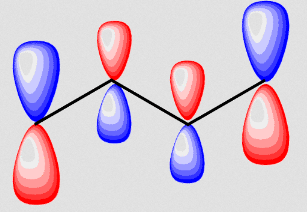
In essence this is similar to simply placing two ethene antibonding molecular orbitals side by side.
Since the left and right halves of the molecule then resemble ethene's antibonding molecular orbital, that suggests reactivity across the double bonds, which is sensible.
Furthermore, since the orbitals are larger at the end-carbons, an added electrophile will bind to the end atom preferentially, which also makes sense to generate a resonance-stabilized carbocation.
ALLYL CATION/ANION
For the allyl cation, try drawing an MO diagram for the allyl radical first. The determinant you should come up with is:
|(stackrel(" "" ""C"_1)stackrel(" ")(""^("C"_1)" "x),stackrel("C"_2)stackrel(" ")1,stackrel("C"_3)stackrel(" ")0),(""^("C"_2)" "1,x,1),(""^("C"_3)" "0,1,x)| = 0
Here I've corresponded which carbon is where on the determinant. Inter-atomic interactions are labeled as "
The substitution is
0 = |(x,1,0),(1,x,1),(0,1,x)| = x|(x,1),(1,x)| - 1|(1,1),(0,x)| + cancel(0|(1,x),(0,1)|)^(0)
0 = x(x^2 - 1) - x
= x[(x^2 - 1) - 1]
= x(x^2 - 2)
Therefore,
E_1 = alpha + sqrt2beta
E_2 = alpha
E_3 = alpha - sqrt2beta
This gives an MO diagram for allyl cation, which uncoincidentally I will make look like that for the allyl radical (which had three
The molecular orbital for
This suggests reactivity on the end-carbons. The MO diagram for the allyl anion is identical except for two additional
The main difference then is that due to adding two
As a result, the allyl anion is more reactive at the central carbon than the allyl cation would be. This makes sense because it often forms an
FORMATE
Here we only examine the
A major difference is that the expansion coefficients in the wave function for the oxygen atoms are larger than for the central carbon (since oxygen is more electronegative), so the orbitals are larger on oxygen than on carbon.
Thus, under the Huckel approximation, we still get:
However, since coefficients will be larger for oxygen, we can make the connection that it was because the
This leads to
That suggests that one of the oxygens will be the reactive atom. This makes sense because formate would certainly want to get protonated as formic acid is a weak acid.

