Question

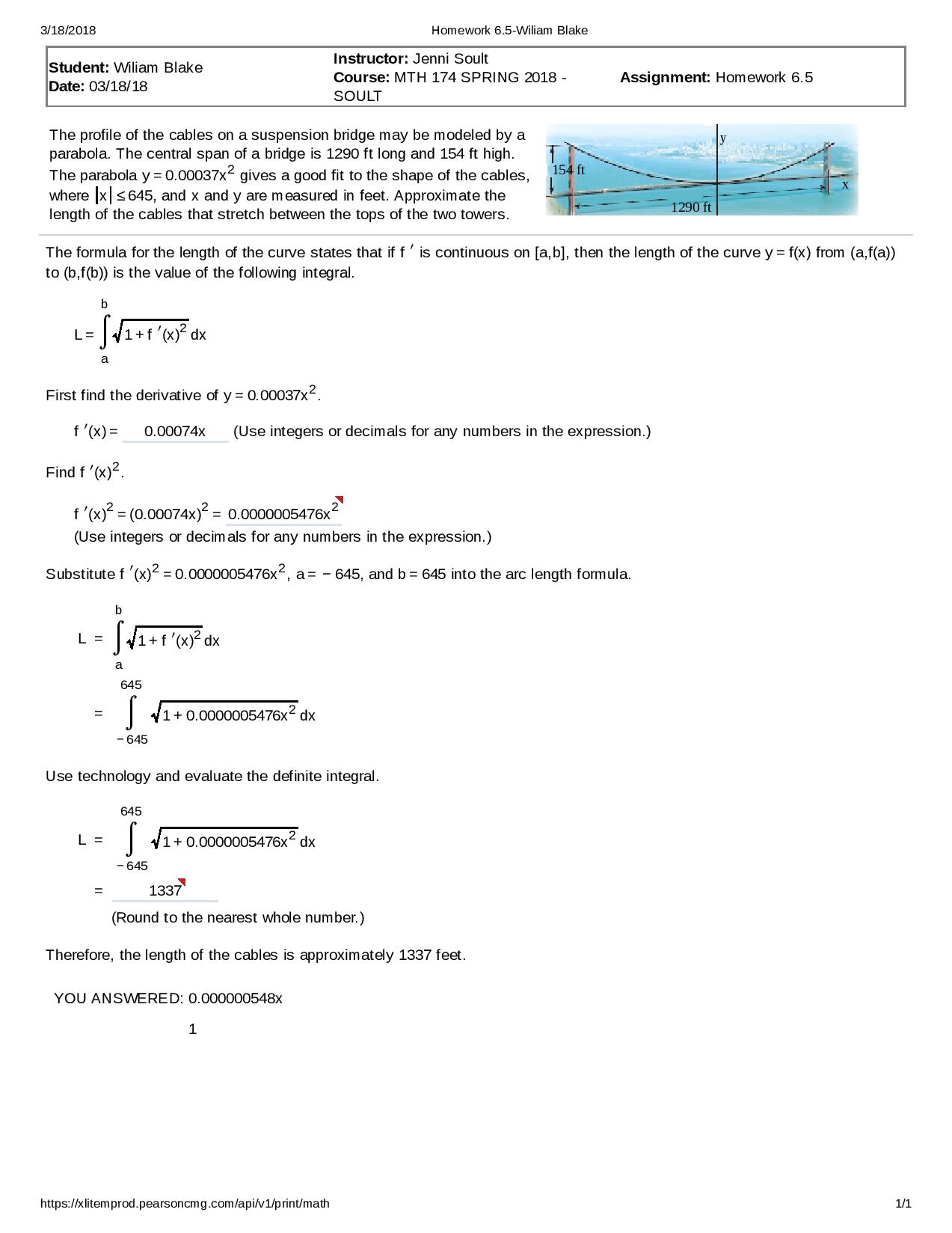
Hi everyone, I am having difficulty in getting the correct answer for some reason. Can someone assist me and explain how to do this properly?

Answer 1

I assume you are happy with the solution provided up to the line that says "Using technology..."
You need to use the technology of Wolfram Alpha, or Simpon's Rule, or integration by substitution, or look it up on the internet.

Explanation:

Use ONE of the following four pieces of technology.
ONE: Using a web brower and using Wolfram Alpha Simpons' Rule Calculator or similar tool:
(i) access http://www.wolframalpha.com/widgets/view.jsp?id=174a81e7a9ffb5aed0a790093981aaab
(ii) fill out the entry form so that it reads;
Use Simpson's Rule to find the approximate value of the integral)#
sqrt(1+0.0000005476*x^2) from x =-645 to x = 645, with interval width equal to 645/2.
(iii) Click on Evaluate and have a coffee.
(iv) Read the pop-up window: "Simpson's rule 1337.43"
(v) Round to the nearest integer: 1337.

OR:
TWO: Use Simpson's rule directly with eight intervals:
Integral = `(h/3)*(f(a)+4*f(a+h)+2*f(a+2h)+4*f(a+3h)+2*f(a+4h)+4*f(a+5h)+2*f(a+6h)+4*f(a+7h)+f(a+8h)`
where `a=-645`, `h=(645-(-645))/8` and `f(x)=sqrt(1+0.0000005476*x^2)`
`=1337.4267004975`

OR
THREE: Access "http://integral-table.com/downloads/single-page-integral-table.pdf" and go down to formula 29:
`int sqrt(x^2+a^2)dx=1/2x*sqrt(x^2+a^2)+1/2*a^2*ln|x+sqrt(x^2+a)|`
and fiddle around with it by getting a suitable value for `a`.

OR
FOUR: Derive formula 29 by substituting `x=tan theta`:

then proceed as for step 3.