Heat transfer... variable area. ?

1 Answer
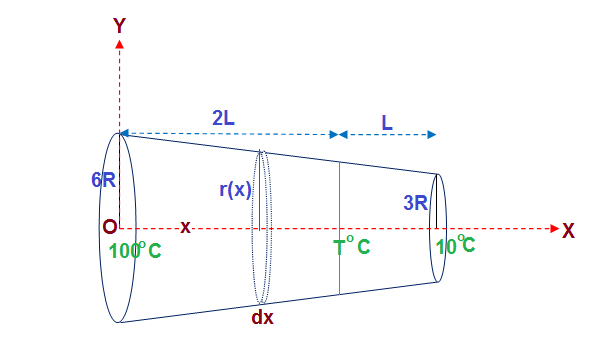
For the sake of computation let us consider that the the center of the left circular surface as origin
Here radius of the thermal resistor decreases with respect to its length at the rate of
Expressing radius of circular cross section as function of
#r(x)=(6 R-R/Lx)#
And area of cross section as function of
#A(x)=pi(6R-R/Lx)^2# .......(1)
Now let
So the rate of heat transfer through a slice of infinitesimal thickness
#Q=-(A(x)kd theta)/(dx)#
where#d theta# represents decrease in temperature across the slice#dx# considered. Here#k# represents the thermal conductivity of the material of the truncated cone.
So
#Q(dx)/(A(x))=-kd theta#
Using (1) we get
#color(magenta)(Q/pi(dx)/(6R-R/Lx)^2=-kd theta)# ......(2)
To find temperature at a particular value of
Let
#dz=-R/L dx#
With this substitution (2) becomes
#-(QL)/(Rpi)(dz)/z^2=-kd theta#
The revised required limits for integration are
For
for
and when
Integrating (3) for first set of limits we get
#(QL)/(Rpi)int_(6R)^(4R)(dz)/z^2=kint_100^Td theta#
#=>(-QL)/(Rpi)[1/z]_(6R)^(4R)=k[theta]_100^T#
#=>(-QL)/(Rpi)[1/(4R)-1/(6R)]=k(T-100)#
#=>color(blue)((-QL)/(Rpi)[1/(12R)]=k(T-100))# ........(4)
Similarly for second set of limits we have
#(QL)/(Rpi)int_(4R)^(3R)(dz)/z^2=kint_T^10 d theta#
#=>(-QL)/(Rpi)[1/z]_(4R)^(3R)=k[theta]_T ^10#
#=>(-QL)/(Rpi)[1/(3R)-1/(4R)]=k(10-T)#
#=>color(green)((-QL)/(Rpi)[1/(12R)]=k(10-T))# .......(5)
Observing that LHSs of (4) and (5) are equal. So equating RHSs which must also be equal we get
#k(T-100)=k(10-T)#
#T-100=10-T#

