Question

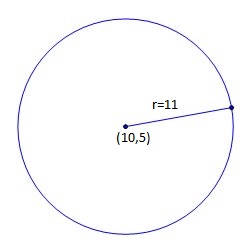
How do you find the equation of the circle given center at the (10, 5) and a radius of 11?

Answer 1

`(x-10)^2+(y-5)^2=121`

Explanation:

`"the standard form of the equation of a circle is"`

`color(red)(bar(ul(|color(white)(2/2)color(black)((x-a)^2+(y-b)^2=r^2)color(white)(2/2)|)))`

`"where "(a,b)" are the coordinates of the centre and r is"`
`"the radius"`

`"here "(a,b)=(10,5)" and "r=11`

`rArr(x-10)^2+(y-5)^2=121larrcolor(red)"equation of circle"`

Answer 2

`x^2+y^2-20x-10y-4=0`

Explanation:

To find the equation of a circle whose radius and center has been given, we have a formula,
`(x-h)^2+(y-k)^2=r^2`
where, `h` and `k` are the x-coordinate and y-coordinate of the center and `r` is the radius.

So,
`(x-10)^2+(y-5)^2=11^2`
`x^2-20x+100+y^2-10y+25=121`
`x^2+y^2-20x-10y-4=0`

Hope this helps :)