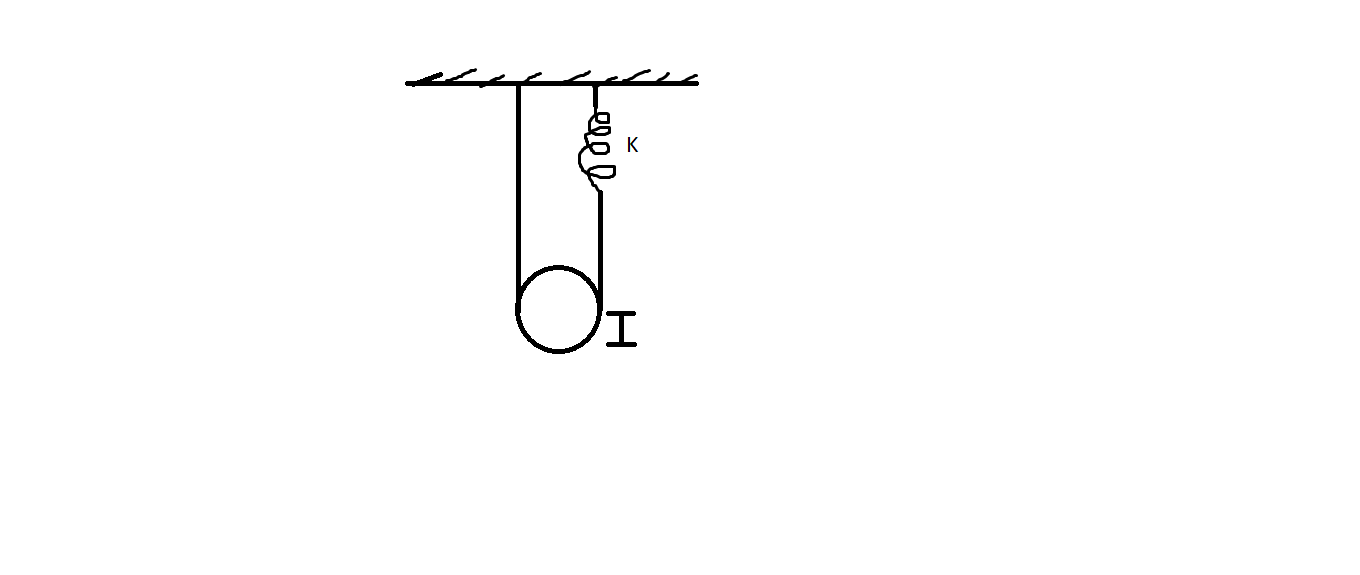
The pulley shown in the figure has a moment of inertia I about its axis and mass m. Find the time period of vertical oscillation of its center of mass. The spring has spring constant K and the string does not slip on the pulley?
 Made from my PC
Made from my PC
 Made from my PC
Made from my PC
1 Answer
Mar 20, 2018
See below.
Explanation:
Assuming the pulley of uniform material.
Pulley dynamics
then solving
we obtain
but
now considering the homogeneous differential equation
obtaining
period

