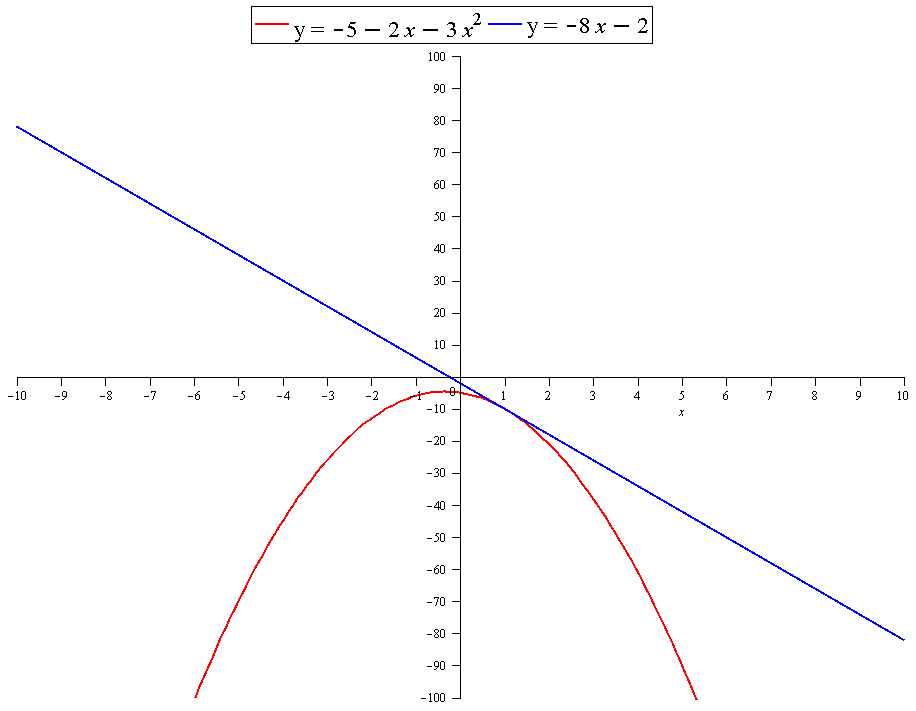
Find an equation of the tangent line?
to the curve y= −5−2x−3x^2 at (1,−10).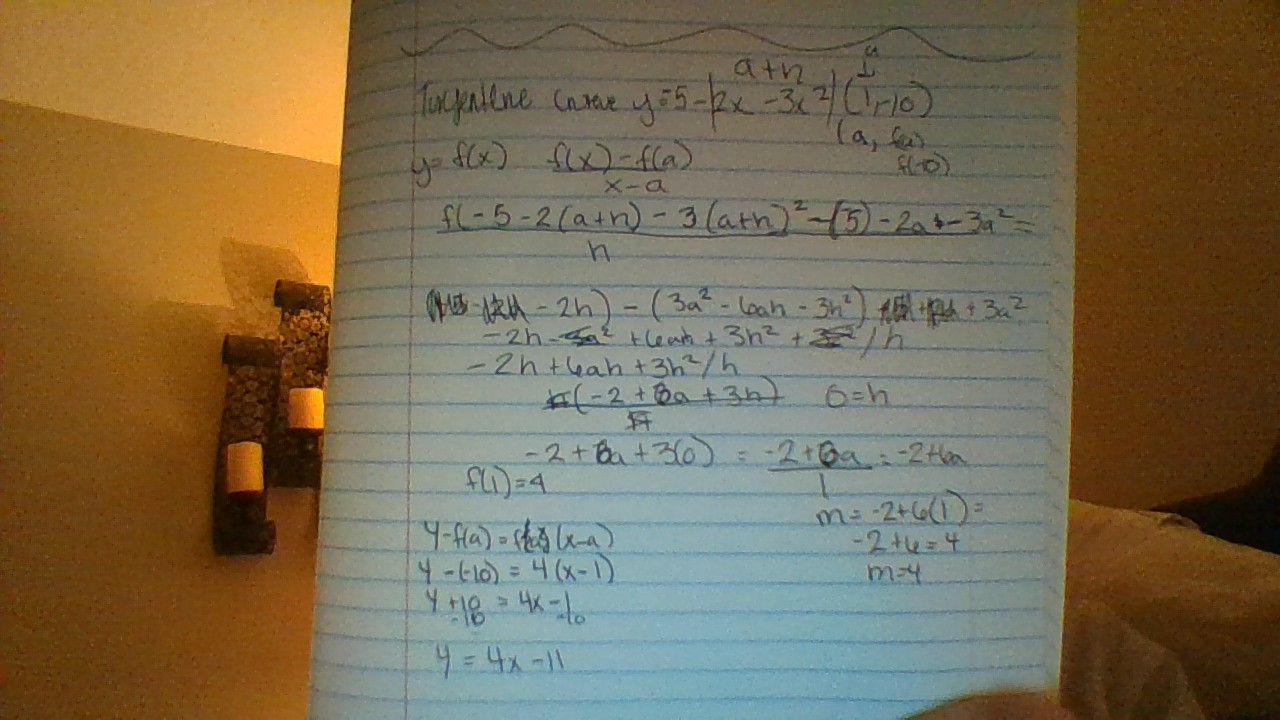
to the curve y= −5−2x−3x^2 at (1,−10).
2 Answers
see below....
Explanation:
#y=-5-2x-3x^2#
#=>(dy)/(dx)=d/(dx)(-5-2x-3x^2)#
#=>(dy)/(dx)=-2-6x" "# [Using the rule#color(red)(d/(dx)x^n=n cdot x^(n-1)# ]
#=>(dy)/(dx)=-2-6 cdot 1=-8#
- The gradient of the tangent is
#-8# The equation of line is
#(y+10)/(x-1)=-8#
#=>y+10=-8x+8#
#=>color(red)(ul(bar(|color(green)(8x+y+2=0)|#
Explanation:
To find the equation of the tangent line to a given point, we first find the first derivative. This will allow us to find the gradient of the tangent line at the given point.
Plugging in
So gradient
Using point slope form of a line:
We have a point on the line
Plugging in these values and the gradient value:
This is the equation of the tangent line to the point
The graph confirms this result: