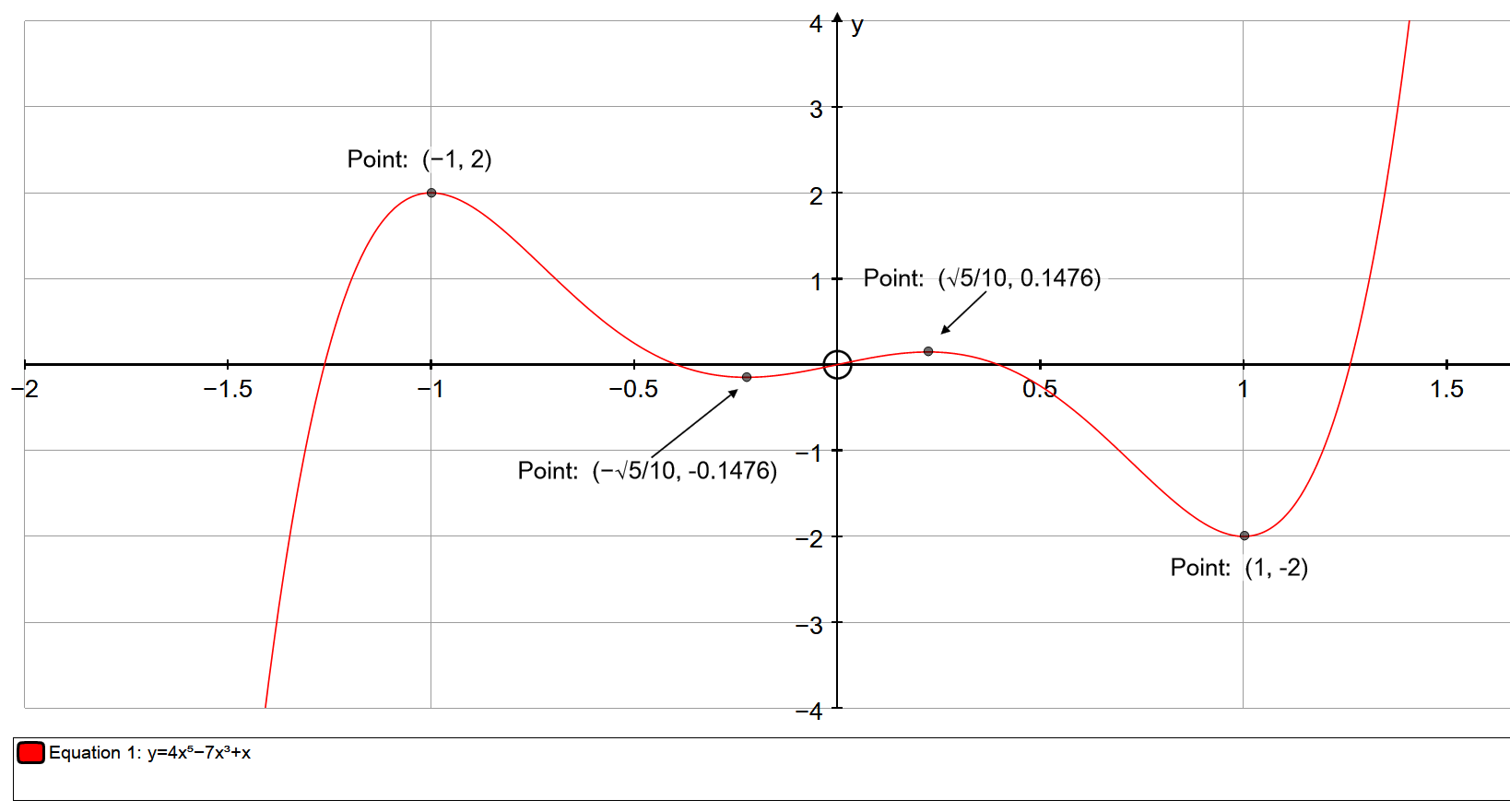
To find critical point we first have to find the first derivative of #h(x)#.
Derivative:
Using the power rule:
#d/dx(ax^n)=anx^(n-1)#
Since the derivative is distributive over the sum, we can use this on each term of the function:
#d/dx(4x^5-7x^3+x)=(5)4x^(5-1) +(3)(-7)x^(3-1)+(1)x^(1-1)#
#=20x^4-21x^2+1#
Maximum/minimum and some inflection point have a gradient of zero. We can find these by equating the derivative to zero:
#20x^4-21x^2+1=0#
Let #z=x^2#, then:
#20z^2-21z+1=0#
Factor:
#(20z-1)(z-1)=0=>z=1/20 and z=1#
But:
#z=x^2#
#:.#
#x^2=1/20=>x=sqrt(5)/10 and x=-sqrt(5)/10#
#x^2=1=>x=1 and x=-1#
We now need to test these value to identify whether they are max/min or inflection points. We know that if:
#f'' > 0 \ \ \ \ \ \ # minimum point.
#f'' < 0\ \ \ \ \ \ # maximum point.
#f''=0\ \ \ \ \ \ # maximum/minimum or point of inflection
This would have to be tested using the first derivative.
The second derivative of #h(x)# is just the derivative of the first derivative. So:
#(d^2)/dx^2(h(x))=d/dx(20x^4-21x^2+1)=80x^3-42x#
Testing values in the derivative:
#x=sqrt(5)/10#
#80(sqrt(5)/10)^3-42(sqrt(5)/10)<0#
#color(blue)(x=sqrt(5)/10) \ \ \ \ \ \ \ # Maximum point
#x=-sqrt(5)/10#
#80(-sqrt(5)/10)^3-42(-sqrt(5)/10)>0#
#color(blue)(x=-sqrt(5)/10) \ \ \ \ \ \ # Minimum point
#x=1#
#80(1)^3-42(1)>0 #
#color(blue)(x=1) \ \ \ \ \ #Minimum point
#x=-1#
#80(-1)^3-42(-1)< 0#
#color(blue)(x=-1) \ \ \ \ \ # Maximum point
We can find inflection points using the second derivative. The function is convex where the second derivative is #>0# and concave where it is #<0#. The concavity changes at points of inflection.
#:.#
#80x^3-42x>0#
#x(80x^2-42)>0#
#(-sqrt(210)/20,0)uu(0,oo)#
#80x^3-42x<0#
#x(80x^2-42)<0#
#(-oo,0)uu(0,sqrt(210)/20)#
We can see from this that there are inflection points at:
#color(blue)(x=0 ,x=(sqrt(210))/20 , x=-(sqrt(210))/20#
GRAPH: