Question

Given `a_3=5` and `a_5=1` in an arithmetic sequence, what is `a_1` and `d`?

Answer 1

`"First Term " a_1 = 9, " Common Difference " d = -2`

Explanation:

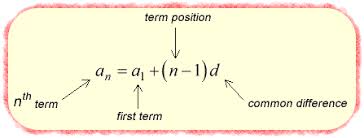https://www.chilimath.com/lessons/intermediate-algebra/arithmetic-sequence-formula/

Given `a_3 = 5, a_5 = 1, " To find First Term " a_1, " common difference " d`

`a_3 = a_1 + (3 - 1) * d`

`a_1 + 2 d = 5, " Eqn 1 "`

`a_5 = a_1 + (5-1) * d`

`a_1 + 4d = 1, " Eqn 2 "`

Solving equations (1), (2)

`" Eqn 2 - Eqn 1 "`

`4d - 2d = 1 - 5 = -4`

`2 d = -4 " or " d = -2`

Substituting value of d in Eqn (1),

`a_1 + 2 * -2 = 5`

`a_1 = 5 + 4 = 9`

Answer 2

`a_1= 9` and `d=-2`.

Explanation:

`U_n= a+(n-1)d`

Now plug in the two equation in the question given and then solve simultaneously like shown below

`a_3= a+(3-1)d`

`a_5= a+(5-1)d`

Therefore

`5= a+2d`
`1= a+4d`

---

`4= -2d`

`d=-2`

Now plug one of the equations given in the question as you have already found out `d`

`U_3=a+(3-1)(-2)`

`5=a+2(-2)`

`5=a -4`

`5+4=a`

`a=9`