What is an equation of a circle if the endpoints of one of its diameters are (2,3) and (4,9)?
1 Answer
Explanation:
Since the two given points,
1) The length of the segment (diameter of the circle), and
2) The midpoint of the segment (the center of the circle).
Let's start with the length of the segment:
Using the Pythagorean theorem (
If we plug these in, we get:
We have our diameter of the circle now, but we want the radius so we can write the equation of the circle later:
We'll use this later.
Now, for the midpoint, which is much simpler:
We're going to find the middle of this line, and the center's coordinate pair will be:
This means finding the average between the
There's the center! Now we have all the info we need, and we just need to plug it into the general form of the circle equation:
Where:
We know all of these, so we can just plug them in to get:
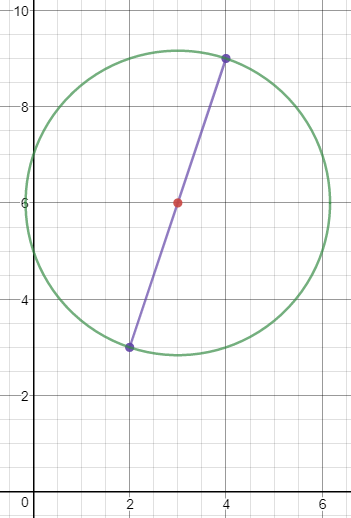
The segment is in purple, the midpoint is in red, and the circle is in green:
 desmos.com
desmos.com

