Question

Triangle ABC is inscribed in a circle that is inscribed in a square. If AB,AC and BC are 8,9 and 10 respectively, determine the exact area of the square? .

Answer 1

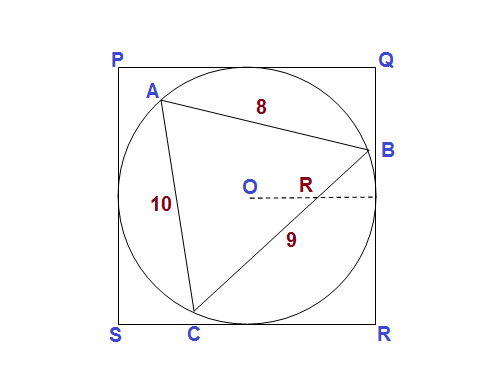
In the figure `Delta ABC` is inscribed in a circle of radius `R` and center `O` and the circle is inscribed in a square `PQRS`.
Obviously the side of the square will be `2R`.

Now in `Delta ABC`,

`BC=a=9,CA=b=10and AB=c=8`

So its semi perimeter `s=(a+b+c)/2=13.5`

So area of `Delta ABC`

`Delta=sqrt(s(s-a)(s-b)(s-c))`

`=>Delta=sqrt(13.5(13.5-9)(13.5-10)(13.5-8))`

`=>Delta=sqrt(13.5xx4.5xx3.5xx5.5)~~34.2` sq unit

Now `R=(abc)/(4Delta)=(9xx10xx8)/(4xx34.2)~~5.17`unit

So area of the square `-4R^2=4xx5.17^2~~107`sq.unit