A projectile is shot at an angle of #pi/4 # and a velocity of # 6 ms^-1#. How far away will the projectile land?
1 Answer
# 3.67 \ m # (3 sf)
Explanation:
For Physics or Mechanics you should learn the "suvat" equations for motion under constant acceleration:
#{: (v=u+at, " where ", s="displacement "(m)), (s=ut+1/2at^2, , u="initial speed "(ms^-1)), (s=1/2(u+v)t, , v="final speed "(ms^-1)), (v^2=u^2+2as, , a="acceleration "(ms^-2)), (s=vt-1/2at^2, , t="time "(s)) :} #
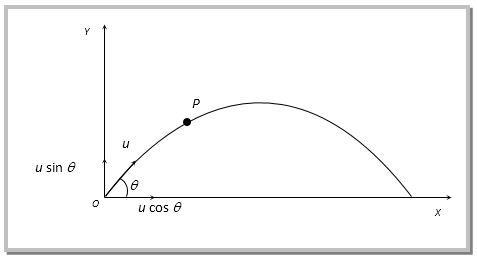
Horizontal Motion
The projectile will move under constant speed (NB we can still use "suvat" equation with
Suppose that the projectile will travel a distance
# { (s=,x,m), (u=,6 cos (pi/4)=3sqrt(2),ms^-1), (v=,"Not Required",ms^-1), (a=,0,ms^-2), (t=,T,s) :} #
So applying
# x = 3sqrt(2)T#
Vertical Motion
The projectile travels under constant acceleration due to gravity. Its displacement will be
# { (s=,0,m), (u=,6 sin (pi/4)=3sqrt(2),ms^-1), (v=,0,ms^-1), (a=,-g,ms^-2), (t=,T,s) :} #
Applying
# 0 = 3sqrt(2)T+1/2(-g)T^2 #
# :. 0 = 6sqrt(2)T-gT^2 #
# :. T(6sqrt(2)-gT) = 0 #
Leading to two possible solution:
# { (T = 0,,"(trivial solution)"),(6sqrt(2)-gT=0,,) :} #
Hence we have:
# 6sqrt(2)-gT = 0 => T = (6sqrt(2))/g #
And using the result we established from the horizontal motion, we have:
# x = 3sqrt(2) * (6sqrt(2))/g#
# \ \ = 36/g#
If we use
# x = 3.67 \ m # (3 sf)

