Question

`f` is some differentiable function. `f'`, the derivative of `f` is shown below [note, is not the graph of f itself]. Use the graph to answer the following questions [For parts (a)-(c), select all that apply]? (See image below)

Answer 1

a. II., III., V. b. I., IV. c. `-4, -2, 1, 3` d. `1` e. `-4, 3`

Explanation:

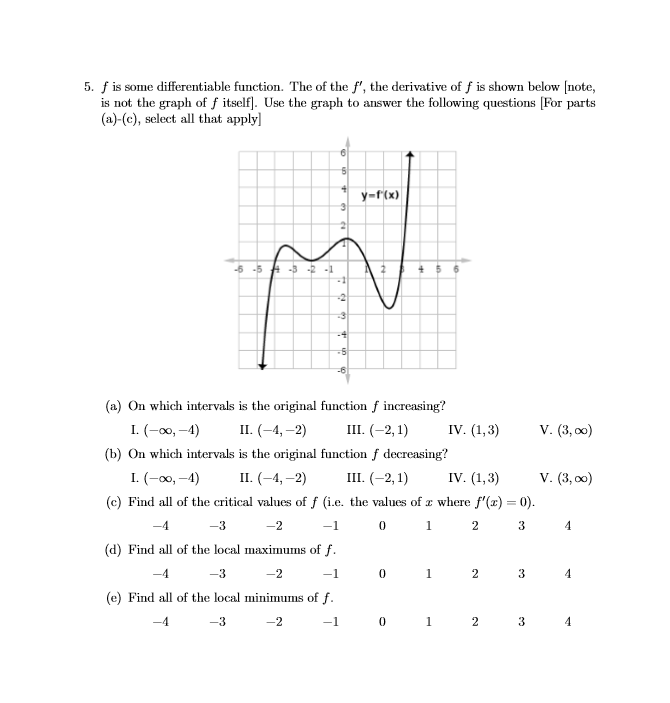
a. `f` increases wherever `f'>0`. Examining the graph, we see `f'>0` on `(-4, 2), (-2,1) (3, oo).` So, the answer is II., III., V.

b. `f` decreases wherever `f'<0`. This holds true for `(-oo, -4), (1, 3).` So, the answer is I., IV.

c. `f'=0` (crosses or touches the `x-`axis) at `x=-4, -2, 1, 3`.

d. A local maximum requires `f'` to change from positive to negative, I.E., `f` to go from increasing to decreasing. `f'` goes from positive to negative at `x=1.`

e. A local minimum requires `f'` to change from negative to positive, I.E., `f` to go from decreasing to increasing. This happens at `x=-4, x=3`

So, we see although `x=2` is a critical value, it is neither a positive or negative. This does happen on occasion; not every critical value is an extreme value.