Solving this electronic problem with impedance ?
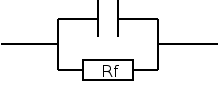
There is two of this image in series, two capacitors C_1 C_2 and two resistors R_1 R_2
To be more precise this is two real capacitors (capacitor and resistor in parallel) in series.
So i have the differential equation etablished by Kirchhoff's laws :
i(1/R_1 + 1/R_2) + (C_1 + C_2)(di)/(dt) = C_1C_2(d^2u)/(dt^2) + (C_2/R_1 + C_1/R_2)(du)/(dt) + u/(R_1R_2)
i tried to do it by impedance because i thought it will take less time.
Impedance of the first real capacitor :
Z_1 = (1/Z_(C_1) + 1/Z_(R_1))^(-1) = Z_(R_1)/(1+Z_(R_1)/(Z_(C_1))
Impedance of the second :
Z_2 = (1/Z_(C_2) + 1/Z_(R_2))^(-1) = Z_(R_2)/(1+Z_(R_2)/(Z_(C_2))
the equivalent impedance of the entire circuit is :
Z_(eq) = Z_1 + Z_2
and then Z_(eq) = u/i
but it lead to
i = 1/R_1(u + R_1C_1jwu) + 1/R_2(u + R_2C_2jwu)
and :
i = u(1/R_1 + 1/R_2) + (du)/dt(C_1+C_2)
j is the imaginary unit
Obviously it's not the same, i know i'm good with Kirchkoff's law because i checked the answer, but i'm not good with impedance, why ?

There is two of this image in series, two capacitors
To be more precise this is two real capacitors (capacitor and resistor in parallel) in series.
So i have the differential equation etablished by Kirchhoff's laws :
i tried to do it by impedance because i thought it will take less time.
Impedance of the first real capacitor :
Impedance of the second :
the equivalent impedance of the entire circuit is :
and then
but it lead to
and :
Obviously it's not the same, i know i'm good with Kirchkoff's law because i checked the answer, but i'm not good with impedance, why ?
1 Answer
See below.
Explanation:
When you solve using impedances you are assuming that the circuit is submitted to a sinusoid periodic input. You are solving without considering the transient modes. So be careful with this approach.

