Find the extremums of the function? #y^2+2x2y+4x-3=0# Thanks much..
3 Answers
Please see below.
Explanation:
.
We solve for
To find the extrema of the function, we take its derivative, set it equal to
This indicates that there are no solutions for
We know that the slope of a tangent line to a curve at a specific point can be found by evaluating its derivative at that point. Since the function does not have any extrema and it is of higher order than one, it must have aymptotes.
This means that the asymptotes are tangent to the curve at
To evaluate the derivative at
This means there are two asymptotes with slopes of
If we repeat the above process for:
we will obtain the results of
In order to find the equation of the oblique asymptote, we will make it much easier if we could avoid dealing with radicals. As such, we will find
As you can see, this is a straight line with slope
Now, we can graph both asymptotes first, then find the coordinates of a number of points using the equation of the function and connect them to construct the full graph as shown below:
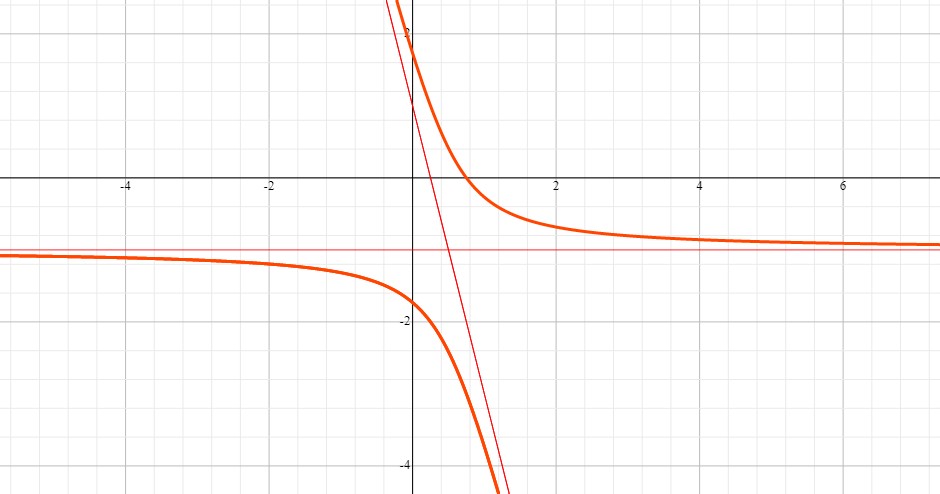
The function is a hyperbola with the center located at the intersection of the two asymptotes.
We can find the center by setting the equations of the asymptotes equal to each other and solving for
In order to find the equation of this hyperbola in its standard form, we would have to get rid of the
That process requires rotation of the coordinates axes by an angle
I spared us from the pain.
Explanation:
.
Hi Lany,
I am finally getting the chance to look at the problem you sent me. I am not sure what you meant to input. Especially, at the bottom I was not sure what you indicated for the interval of
So, I am going to make some guesses and try to figure this out based on some assumptions on my part.
In the cartesian coordinate system, the increment of the area
In the polar coordinate system,
In your problem, the integral is in the cartesian coordinate system:
with the following boundary information(as far as I could figure out):
The region
The last piece was unclear to me. I will just use
Let's see what this region looks like. We will graph
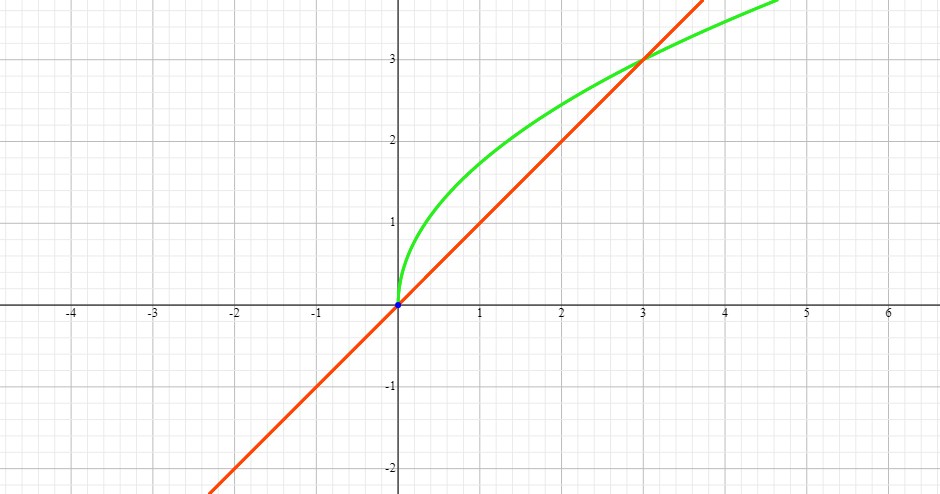
So, the region lies in between the two curves. Now let's graph
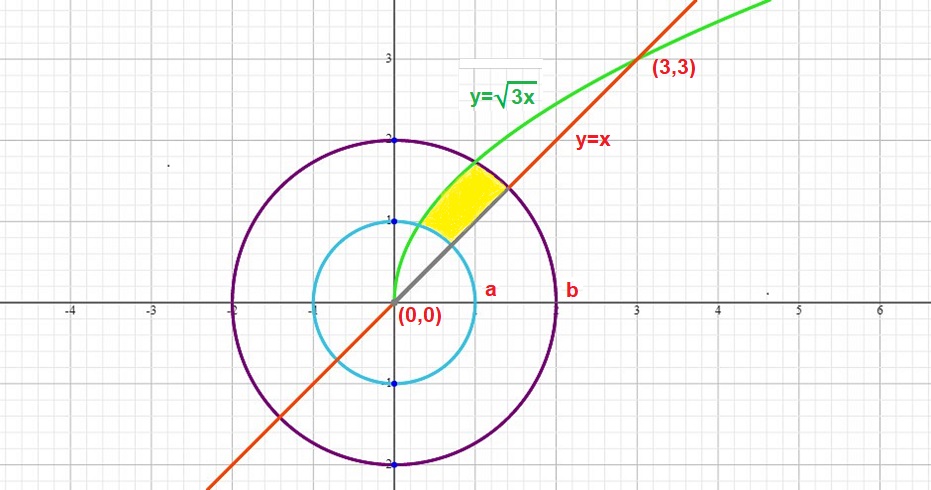
These two circles further restrict
The given integral calculates the volume of a solid that has the yellow area
Let's look at the graph of the function inside the integral with
The real part is:
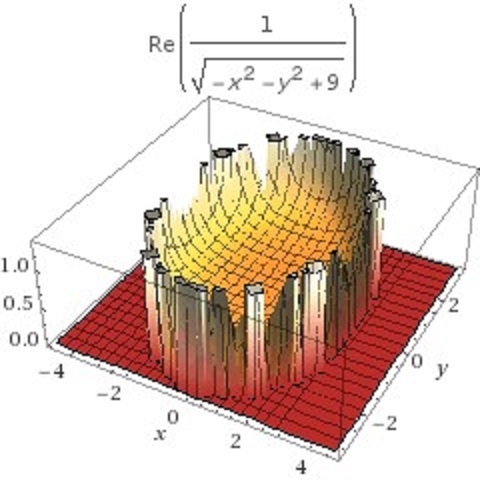
The imaginary part is:
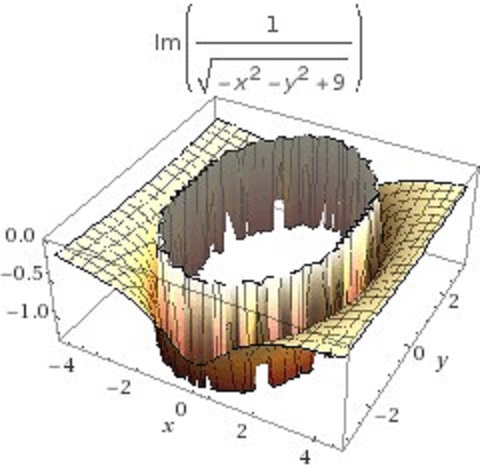
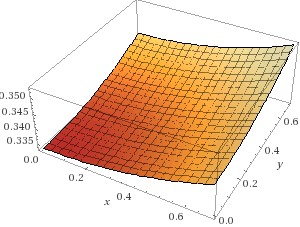
Imagine the yellow shaded region
Additionally, imagine two
The volume of the piece bounded by the cylinder I described above and these two planes is the result of the integral given in our problem. It looks like this:
Let's convert the integral to a polar one:
We set the two given boundary functions equal to each other and solve for their intersection points:
In a polar system:
Let
There are no critical points but the function has critical point behaviour at its asymptotes of
Explanation:
We have:
# y^2+2x2y + 4x-3=0 #
Differentiating implicitly wrt
# 2y dy/dx + 4(xdy/dx+y)+4 = 0 #
At an extremum, or critical point, the first derivative vanishes, so putting
# 0 + 4(0+y)+4 = 0 => 4y+4 = 0 #
# " " => y=-1#
Substituting
# 1-4x + 4x-3=0 => 0 =0 => # no#y# solution
If we examine the graph of the function, this becomes clear as
graph{y^2+2x2y + 4x-3=0 [-10, 10, -5, 5]}


