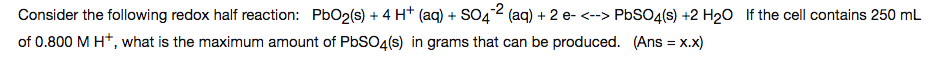We have the following redox half-reaction, where lead (Pb) is reduced from Pb(IV) to Pb(II):
PbO_2(s)+4H^+(aq)+SO_4^(2-)(aq)+2e^(-)rightleftharpoonsPbSO_4(s)+2H_2O(l)
We are given 250 \ "mL" of 0.8 \ "M" of hydrogen ions. Let's convert that to moles.
Molarity is given by:
"molarity"="moles of solute"/"liters of solution"
And so,
0.8 \ "M"="moles of solute"/(0.25 \ "L")
"moles of solute"=0.2 \ "mol"
So, we got 0.2 moles of hydrogen ions.
According to the equation, four hydrogen ions produce one molecule of lead(II) sulfate, and so here, we would produce:
0.2color(red)cancelcolor(black)("mol of" \ H^+)*(1 \ "mol of" \ PbSO_4)/(4color(red)cancelcolor(black)("mol of" \ H^+))=0.05 \ "mol of" \ PbSO_4
Lead(II) sulfate has a molar mass of 303.26 \ "g/mol".
So here, we got:
0.05color(red)cancelcolor(black)"mol"*(303.26 \ "g")/(color(red)cancelcolor(black)"mol")=15.163 \ "g"
~~15.2 \ "g"
I rounded the answer to one decimal place, since the answer box also requires the answer to be in one decimal place.