How to find these type of question easily, without using L-hopitals rule?

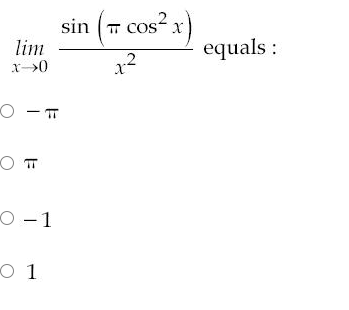
enter image source here

2 Answers
Cesareo R.
Apr 2, 2018

#pi#

Explanation:

#sin(pi cos^2 x)/x^2 = sin(pi -pi sin^2)/x^2 = sin(pi sin^2 x)/x^2#

but for small #abs x# we have #sinx = x -x^3/(3!) + O(x^5)# and also

#sin^2 x = x^2+ O(x^4)# hence

#lim_(x->0)sin(pi cos^2 x)/x^2 =lim_(x->0)sin(pi(x^2+O(x^4)))/x^2 = pi lim_(x->0)sin(pi(x^2+O(x^4)))/(pix^2) = pi#

Jim H
Apr 2, 2018

Please see below.

Explanation:

As Cesareo points out:

#sin(pi cos^2 x)/x^2 = sin(pi(1 - sin^2))/x^2#

# = sin(pi -pi sin^2)/x^2# #" "# (now use the difference formula)

# = sin(pi sin^2 x)/x^2#

# = sin(pi sin^2 x)/1 1/x^2#

# = sin(pi sin^2 x)/(pisin^2x) (pisin^2x)/x^2#

# = sin(theta)/(theta) pi (sinx/x)^2#

At #xrarr0#, we also have #theta rarr0#, so the limit is

#1(pi)(1)^2 = pi#

Related questions
Impact of this question
1298 views around the world
You can reuse this answer
Creative Commons License