Question

Can you solve the equation for this interval [0, 2pi]? Sin(2x-(pi/4)) = (sqrt2)/(2)

Answer 1

`x = pi/4, pi/2, (5pi)/4, (3pi)/2`

Here's how I did it:

Explanation:

`sin(2x-(pi/4))=sqrt2/2`

First, we can rewrite this with an `sin^-1`
`sin^-1(sqrt2/2) = 2x - pi/4`

From the unit circle, we know that `sin(pi/4) = sqrt2/2`, meaning that `sin^-1(sqrt2/2) = pi/4`:

`pi/4 = 2x - pi/4`

Add `pi/4` to both sides of the equation:
`(2pi)/4 = 2x`
`pi/2 = 2x`

`x = (pi/2)/2`

`x = pi/2 * 1/2`

`x = pi/4`

There is still another solution since sine is also positive in the second quadrant:
To find the other solution, we refer to the unit circle:

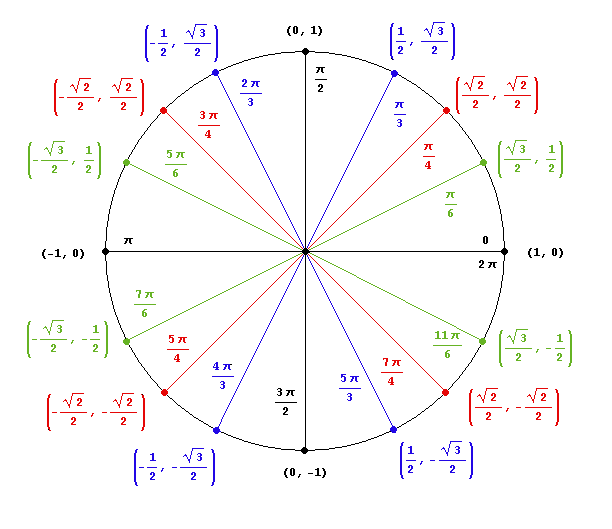
We can see that `sinx = sqrt2/2` also occurs at `(3pi)/4`. So:
`2x-pi/4 = (3pi)/4`

`2x = 4pi/4`

`2x = pi`

`x = pi/2`

So we have `x = pi/4` and `pi/2`.

However, we want the solutions between `[0, 2pi]`.

First, we have to find the period of the function `sin(2x-pi/4)`. Recall that the period of `sinx = 2pi`. In this case, we are finding the period of `sin2x`, so:
`2pi/2 = pi`

The period is `pi`.

This means that we can add `pi` to each of our solutions:
`pi/4 + pi = pi/4 + (4pi)/4 = (5pi)/4`

`pi/2 + pi = pi/2 + (2pi)/2 = (3pi)/2`

We cannot add another `pi` to any of these solutions or else it would go over `[0, 2pi]`

So the final answers are `x = pi/4, pi/2, (5pi)/4, (3pi)/2`.

Hope this helps!

Answer 2

`color(blue)(pi/4 , (3pi)/2 , pi/2 ,(5pi)/4 )`

Explanation:

`sin(2x-pi/4)=sqrt(2)/2`

`arcsin(sin(2x-pi/4))=arcsin(sqrt(2)/2)=pi/4+n2pi,(3pi)/4+n2pi`

`2x-pi/4=pi/4+n2pi`

`2x=pi/2+n2pi`

`x=pi/4+npi`

`2x-pi/4=(3pi)/4+n2pi`

`2x=pi+n2pi`

`x=pi/2+npi`

For:

`[0,2pi]`

`color(blue)(pi/4 , (3pi)/2 , pi/2 ,(5pi)/4 )`