Why isn't this triangle an ambiguous case? (where there can be 2 possible triangles from the same set of lengths and an angle)
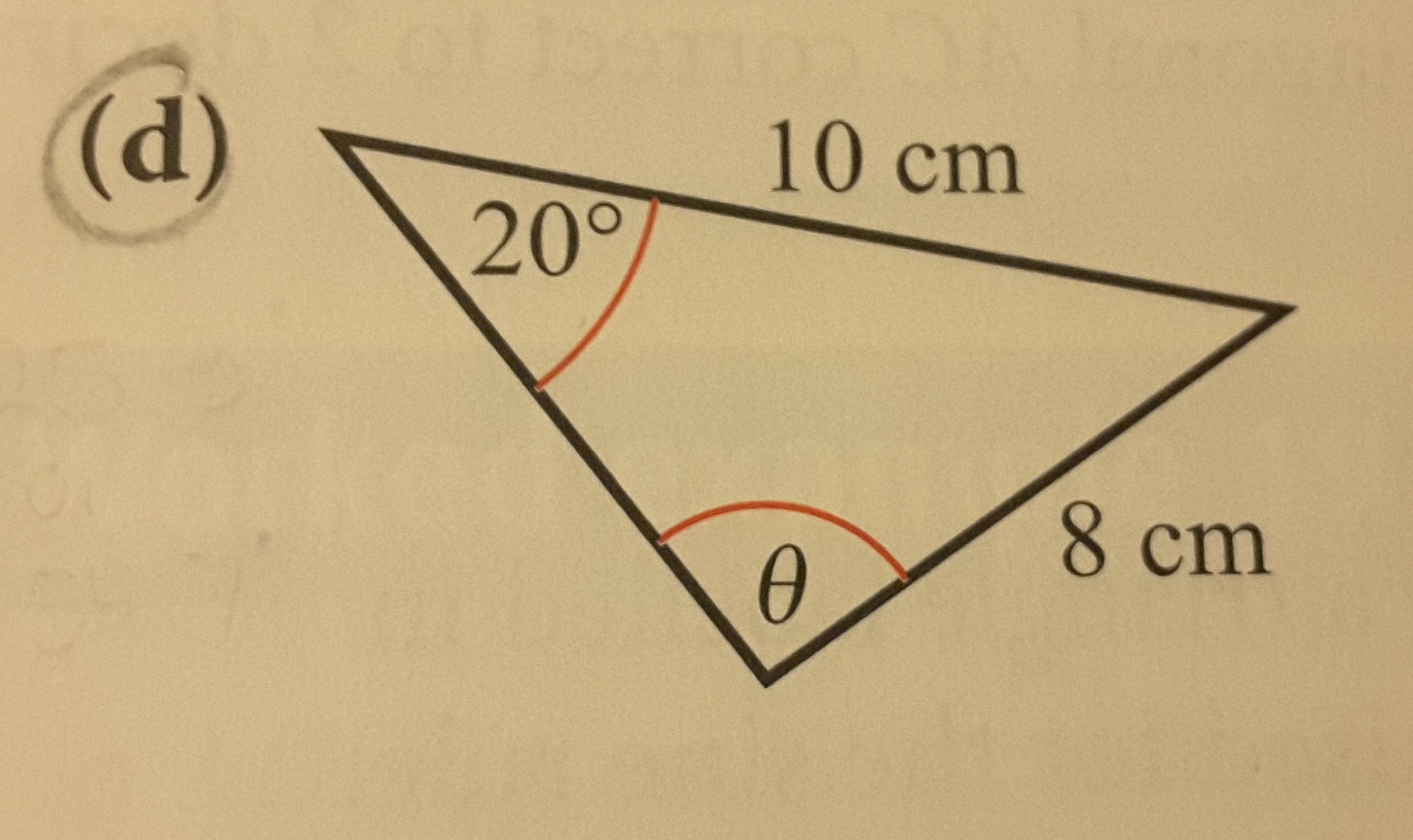
I've figured out the height of the triangle #h=3.4202# and since that ambiguous cases happen when #h< a< b# where #a# is the length opposite of a given length and #b# is some other length, shouldn't this triangle have 2 possible answers?
I'm terribly new to the whole subject of ambiguous cases so any help would be greatly appreciated!
Thanks in advance!

I've figured out the height of the triangle
I'm terribly new to the whole subject of ambiguous cases so any help would be greatly appreciated!
Thanks in advance!
1 Answer
See below.
Explanation:
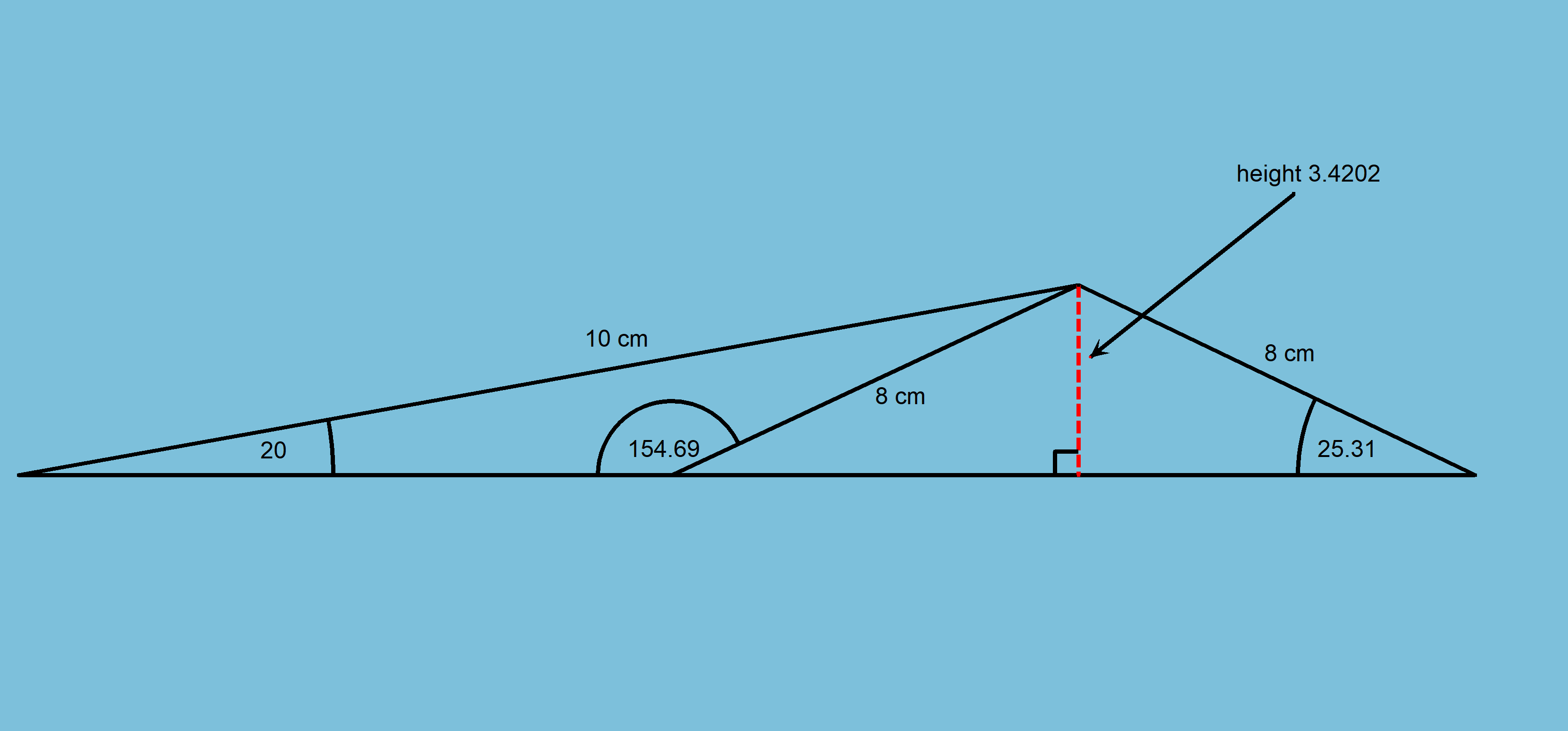
This is your triangle. As you can see it is an ambiguous case.
So to find the angle
Because it's the ambiguous case:
Angles on a straight line add to
You can see from the diagram that, as you noted:
Here is a link that may help you. This can take a while to grasp, but you seem to be on the right track.
http://www.softschools.com/math/calculus/the_ambiguous_case_of_the_law_of_sines/

