Write the complex number #(-1-i)^6# on the #re^θ = r(cos θ + i sin θ)# form (polar form) and the #a+ ib# form?
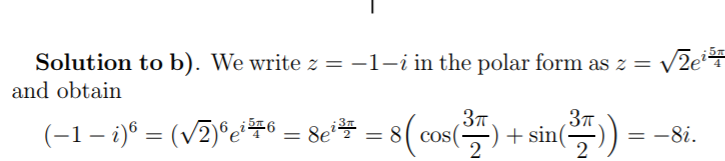
This is the solution, but can someone explain how this happen?
This is the solution, but can someone explain how this happen?
1 Answer
Apr 10, 2018
We know
However, as
We now have
In terms of rotation

