Question

If the first derivative has a cusp at x=3, is there a point of inflection at x=3 even though the second derivative doesn't exist there?

Answer 1

It depends, in part, on the definition of inflection point being used.

Explanation:

I have seen some who insist that the second derivative must exist to have an IP.

I am more used to the definition:

An inflection point is a point on the graph at which concavity changes..

So I consider the point `(0,0)` an inflection point for `f(x) = root(3)x` in spite of the non-existence of `f'(0)` and `f''(0)`.

Similarly, the function `f(x) = 1/2xabsx` has derivative `f'(x)=absx`. So the derivative has a cusp at `0`.
Since the graph of `f` is concave down on `(-oo,0)` and concave up on `(0,oo)` and `f(0)` exists (it is `= 0`), I count `(0,0)` as an inflection point.

In the graph below, you see `f` in blue, `f'` in red and `f''` in orange.

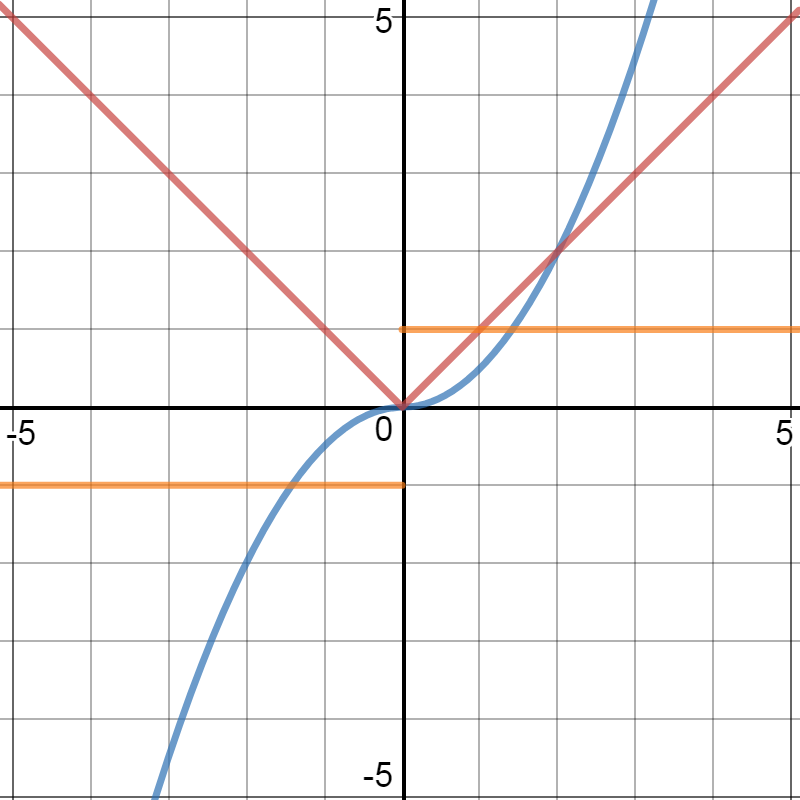
Translate 3 to the right to get an example at `3`.