Question

Find the speed of the cylinder as it falls through a distance h?

A cylinder of mass m is suspended through two strings wrapped around it as shown in fig.
Find the speed of the cylinder as it falls through a distance h.

Answer 1

`T = 1/6 mg`

`v = 2 sqrt((gh)/3)`

Explanation:

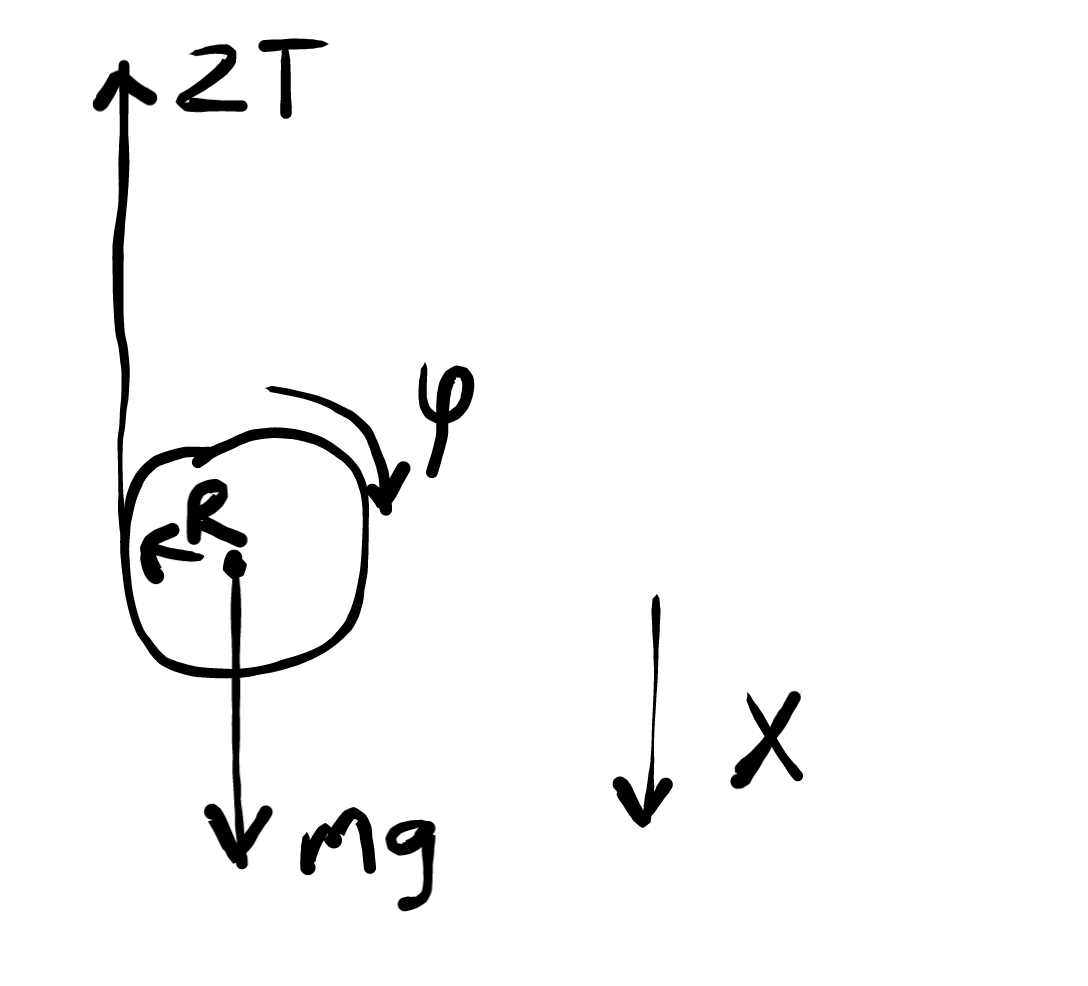
This is idealised, eg assumes that the strings remain in the vertical position.

But this does serve as a FBD. With `x` as the key co-ordinate, which is positive pointing downward:

• Newton's 2nd law in the `x` direction:

`m a = sum F implies m a = mg - 2T qquad triangle`

• Newton's analogous 2nd law for rotation: ie Taking moments/looking at torques about the centre of the cylinder:

`I alpha = sum tau implies I alpha = 2 T R qquad square`

For the cylinder: `I = 1/2 m R^2`; and from the geometry: `R psi = x implies a = R alpha`.

It follows from `square` that:

`T =( I alpha)/(2R) = ( 1/2m R^2 ( a)/R)/(2R) = 1/4 m a qquad circ`

Plugging this into `triangle`:

`m a = mg - 2( 1/4 m a) implies a = 2/3 g qquad star`

Finally, from `circ`:

`T = 1/4 ma = 1/6 mg` <-- that's a)

For the next part, assuming you mean final velocity having fallen from rest through a height `h`, from `star` we have `a = 2/3 g`. If you remember your SUVAT equations:

`v^2 = u^2 + 2 a s`

So here:

`v = sqrt(0 + 2 (2/3 g)h) = 2 sqrt((gh)/3)`