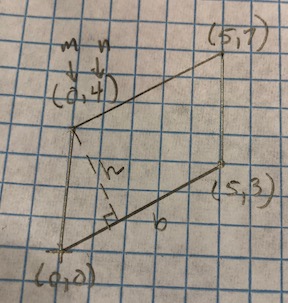Given: coordinates of a parallelogram. Find area.
#A = bh#
It's easiest to show by actually doing an example.
Example: #(0, 0), (5, 3), (5, 7), (0, 4)#. The points #(0, 0), (5,3)# represent the base. The point #(0, 4) = (m, n) -> " left top"#
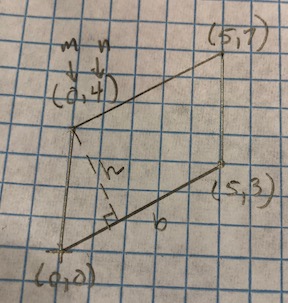
Find the length of the base #b# using the distance formula:
#d = sqrt((y_2-y_1)^2 + (x_2 - x_1)^2)#
#b = sqrt((3-0)^2 + (5-0)^2) = sqrt(9 + 25) = sqrt(34)#
Find the height #h# using the perpendicular distance from a line to a point formula:
#d =( |Am + Bn + C|)/sqrt(A^2 + B^2)# where #(m, n)# is the left-top point we will use to drop a perpendicular to the line of the base #b#.
The line that represents the base needs to have the form: #Ax + By + C = 0#
Find the line for the base:
#"slope" = m = (3-0)/(5-0) = 3/5#
Line: #y - y_1 = m ( x - x_1); " "y - 3 = 3/5 (x - 5)#
Distribute:
#y - 3= 3/5 x + 3/5* -5/1; " "y - 3 = 3/5 x -3#
Base line: #y = 3/5 x#
Base line in #Ax + By + C = 0# form:
#3/5 x -y = 0; " " 5(3/5 x - y = 0) = 3x - 5y = 0#
#A = 3; " " B = -5; " " C = 0#
#h =( |3*0 + (-5)*4 + 0|)/sqrt(3^2 + (-5)^2) = |-20|/(sqrt(9 + 25)#
#h = 20/sqrt(34)#
#A = bh = sqrt(34) * 20/sqrt(34) = 20 " units"^2#