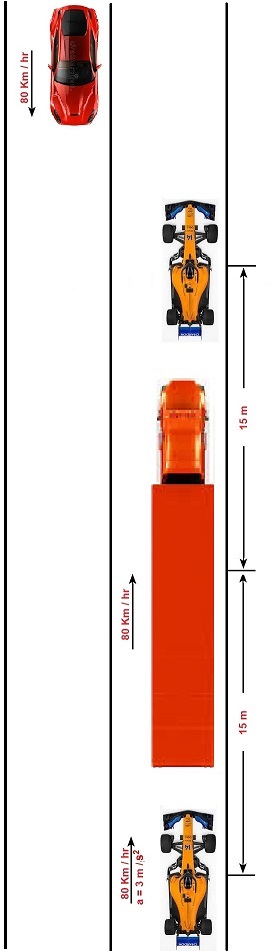
On a two-lane highway, a car is 15m behind a truck (distance between midpoints), both traveling at 80 km/h. The car has a maximum acceleration of 3m/s^2. The driver of the car wants to pass the truck and be back in the right line 15m ahead of the truck?

On a two-lane highway, a car is 15m behind a truck (distance between midpoints), both traveling at 80 km/h. The car has a maximum acceleration of 3m/s^2. The driver of the car wants to pass the truck and be back in the right line 15m ahead of the truck. At the moment the driver starts overtaking the truck, a car is coming in the opposite direction, also at 80 km/h. What is the minimum safe distance the two cars need to have?

1 Answer
Sean
Apr 14, 2018

#228.76# meters

Explanation:

.

enter image source here

#a(t)=3# #m"/"s^2# This is the car's acceleration.

We need to take the integral of the acceleration function to get the velocity function:

#V(t)=inta(t)dt#

#V(t)=int3dt=3t+c_1#

We use our initial conditions to solve for the constant of the integral. At time #t=0# the velocity is #80" "km"/"h#.

#80# km/h is #((80)(1000))/3600=200/9# meters / second

#V(0)=3(0)+c_1#

#200/9=0+c_1#

#c_1=200/9#

Therefore, the velocity function is:

#V(t)=3t+200/9#

We need to take the integral of the velocity function to get the position function:

#S(t)=intV(t)dt=int(3t+200/9)dt=3/2t^2+200/9t+c_2#

Let's use initial conditions to solve for the constant of integration:

We will consider the position (distance traveled) at #t=0# to be #S(0)=0#. Therefore,

#0=3/2(0)^2+200/9(0)+c_2#

#0=0+0+c_2#

#c_2=0#

#S(t)=3/2t^2+200/9t#

This is the distance the car travels in #t# seconds that it takes to go the same distance the truck travels plus #30# meters (#15# meters behind the truck + #15# meters ahead of the truck)..

The truck travels a distance of #200/9t# in the same #t# seconds.

These distances are equal. We will set them equal to each other and solve for #t#:

#3/2t^2+200/9t=200/9t+30#

#3/2t^2=30#

#3t^2=60#

#t^2=20#

#t=2sqrt5# seconds

This is the time it takes for the car to pass the truck and get ahead of the truck by #15# meters.

The distance the car covers to do this is:

#S(t)=3/2(20)+200/9(2sqrt5)=129.38# meters

In the same time frame, the car coming in the opposite direction covers the distance of:

#200/9(2sqrt5)=99.38# meters

Therefore, the safe distance between the two cars is:

#129.38+99.38=228.76# meters

Related questions
Impact of this question
1700 views around the world
You can reuse this answer
Creative Commons License