intx(x+1)^3dx=?
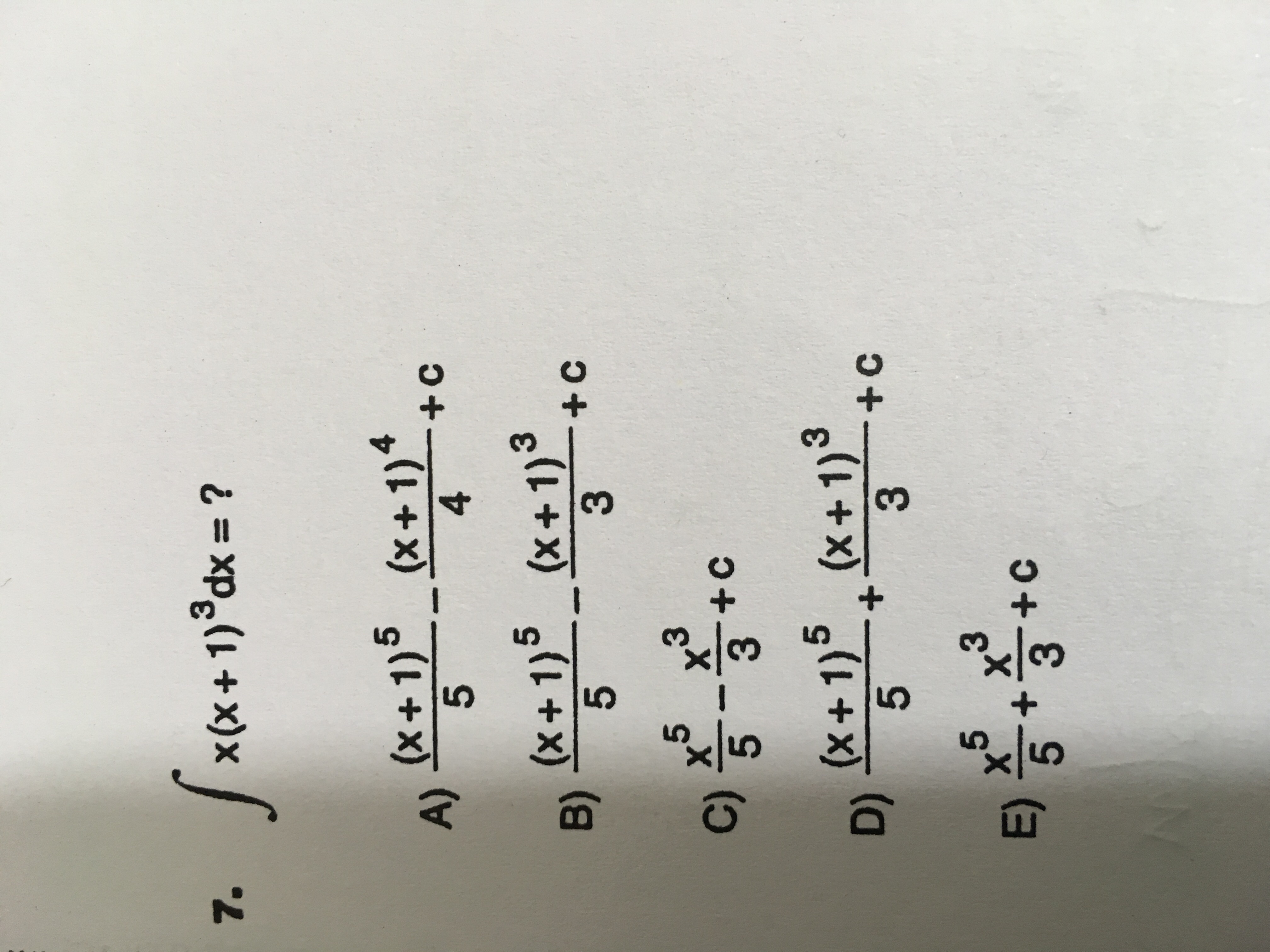
2 Answers
Apr 14, 2018
Explanation:
Approached by
Let
Apr 14, 2018
The answer is
Explanation:
Let
Therefore,
The answer is


