Help with physics momentum problems I have a test tomorrow, please?

1) A toy rocket achieves a velocity of 55 m/s after 3 s, when fired straight up. If the average force exerted by the engine is 28 N, what is the toy’s mass?
2) A 15000 kg air jet accelerates from rest to 45 m/s before it takes off. What is the change in momentum of the jet?
3) A small bouncy ball with a momentum of 8 kg∙m/s to the left approaches head-on a large door at rest. The ball bounces straight back with a momentum of 6 kg∙m/s. What is the change in the momentum of the ball? What is the impulse exerted on the ball? What is the impulse exerted on the door?

2 Answers
sjc
Apr 15, 2018

see below

Explanation:

we need the following results

momentum #=# mass#xx#velocity; and is a vector quantity

Newton's 2nd Law : # F_("net")=ma#

#(1)#

so we have

#F=28N#

#u=0 ms^(-1)#

#v=55ms^(-1)#

#t=3s#

we need to find the acceleration

using

#v=u+at#

#55=0+3a#

#:.a=55/3ms^(-2)#

#N2L#

# F_("net")=ma#

#28=55/3m#

#m=(28xx3)/55=84/55kg#

#(2)

the momentum at the start is zero - at rest #=># no momentum

change of momentum#=15 000xx45-0#

#=675 00" " kgms^(-1)#

#(3)

Impulse #=# change of momentum

taking the original direction of travel as #+ve#

initial momentum#=+8" "kgms^(-1)#

momentum after #=-6" "kgms^(-1)#

change of momentum #=8 --6=14" "kgms^(-1)#

impulse on the ball is opposite to original direction

#:. -14" "kgms^(-1)#

so impulse on door #=+14" "kgms^(-1)#

Tom M.
Apr 15, 2018

a)#1.53 " kg"#
b) #675,000" Ns"#
c) #14" Ns, "14" Ns, "# and #14 " Ns"#

Explanation:

1)

We will assume the acceleration of the rocket is constant.

#"Using " v=u+at# (one of the kinematic "suvat" equations)

#55=0+3a#

#a=55/3 ms^-2#

#"Using Newton's Second Law"#

Newton's Second Law is sometimes written as #F=ma#. It states that the resultant force on an object is equal to its mass times acceleration.

#28=55/3m#

#m=28xx3/55#

#m=84/55#

#=1.53"kg" (3"s.f.")#

2)

The momentum of an object is its mass times its velocity.

#p=mv#
The unit is #"kg ms"^-1# or #Ns# (Newton-seconds). Both of these units are the same, and both can be used interchangeably (I use both in this answer).

For our question:

#"Initial momentum"=15,000xx0#
#=0 " Ns"#

Note how when it is stationary, it has no momentum.

#"Final momentum"=15,000xx45#
#=675,000" Ns"#

#"Change in momentum"=675000-0#
#=675,000" Ns"#

The change in momentum is known as impulse.

3)

Even for simple physics problems like these, where we don't need a diagram, drawing may help.

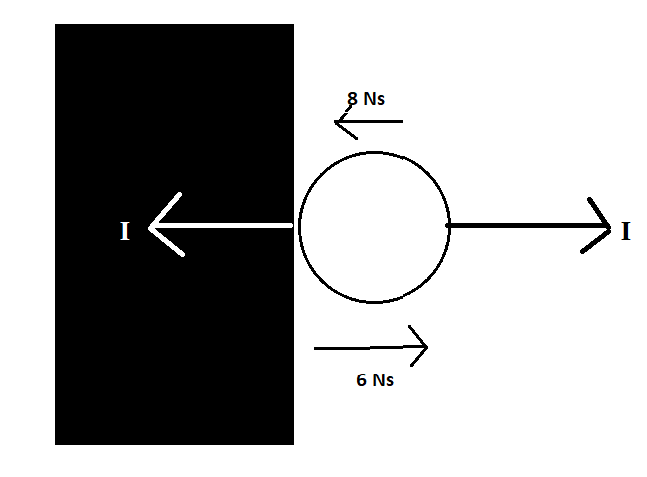
enter image source here

Here, the arrows above and below the ball indicate its momentum (you can do something similar with speeds if given those instead of momentums). The arrows coming out of the ball and into the wall, with an #I# next to them represent the impulse.

Just like how velocity is a vector, and can have plus and minus, so can momentum. Since the final momentum is in the opposite direction to the initial momentum, we will consider this in our calculations as #-6" kg ms"^-1#

#"Change in momentum"=8-(-6)#
#=14" kg ms"^-1#

I touched on this earlier. The Impulse-momentum principle (its scarier than it sounds) states the Impulse=change in momentum.

#"Using the Impulse-momentum principle"#

#I=14" kg ms"^-1#

You may have heard of Newton's Third Law. This states that for every action there is an equal and opposite reaction. Effectively, we use this to mean the impulse on the door is equal and opposite to the impulse on the ball

#"By Newton's Third Law"#

#I=14" kg ms"^-1#

Related questions
Impact of this question
4949 views around the world
You can reuse this answer
Creative Commons License