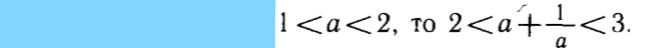Let a=p/q where p and q are positive integers.
1ltp/q therefore qltp. p/qlt2 therefore plt2q. Therefore qltplt2q.
a+1/a=p/q+q/p=(pp)/(qp)+(qq)/(pq)=(p^2+q^2)/(pq)=(p^2+2pq+q^2-2pq)/(pq)=(p+q)^2/(pq)-(2pq)/(pq)=(p+q)^2/(pq)-2
(q+q)^2/(qq)lt(p+q)^2/(pq)lt(2q+q)^2/(2qq)*
(2q)^2/q^2lt(p+q)^2/(pq)lt(3q)^2/(2q^2)
(4q^2)/q^2lt(p+q)^2/(pq)lt(9q^2)/(2q^2)
4lt(p+q)^2/(pq)lt9/2
4-2lt(p+q)^2/(pq)-2lt9/2-2
2lt(p+q)^2/(pq)-2lt5/2
2lta+1/alt5/2
5/2lt6/2
5/2lt3
2lta+1/alt3
~~More advanced topics ahead~~
*This assumes that as p increases, (p+q)^2/(pq) increases. This can be verified intuitively, by looking at the graph of y=(x+q)^2/(xq) on x in(q,2q) for various positive values of q, or by the calculus process below.
~
del/(delp)[(p+q)^2/(pq)]=1/qdel/(delp)[(p+q)^2/p]=1/q(pdel/(delp)[(p+q)^2]-(p+q)^2del/(delp)[p])/p^2=1/q(p[2(p+q)]-(p+q)^2[1])/p^2=1/q(2p(p+q)-(p+q)^2)/p^2=((2p^2+2pq)-(p^2+2pq+q^2))/(p^2q)=(p^2-q^2)/(p^2q).
On p in(q,2q):
Since pgtqgt0, p^2gtq^2 thus p^2-q^2gt0.
Since q>0, p^2qgt0
Since p^2-q^2gt0 and p^2qgt0, (p^2-q^2)/(p^2q)gt0
Since del/(delp)[(p+q)^2/(pq)]=(p^2-q^2)/(p^2q) and (p^2-q^2)/(p^2q)gt0, del/(delp)[(p+q)^2/(pq)]gt0
Therefore (p+q)^2/(pq) is increasing for constant q and qltplt2q because del/(delp)[(p+q)^2/(pq)] is positive.
~~~~