Find the length of the tangents from the origin to tge circle #3x²+3y²+12x+8y+8=0#. Find also the acute angle between the tangents from the origin to the circle (answer#= (2*sqrt6)/3 ,86°#)?

1 Answer
P dilip_k
Apr 17, 2018

enter image source here
Transforming the given equation of the circle #3x²+3y²+12x+8y+8=0# in standard form we get.

#3x²+3y²+12x+8y+8=0#

#=>x²+y²+4x+8/3y+8/3=0#

#=>(x²+2*x*2+ 2^2)+y^2+2*y*4/3+(4/3)^2=4+16/9-8/3#

#=>(x+2)^2+(y+4/3)^2=(sqrt(28/9))^2#

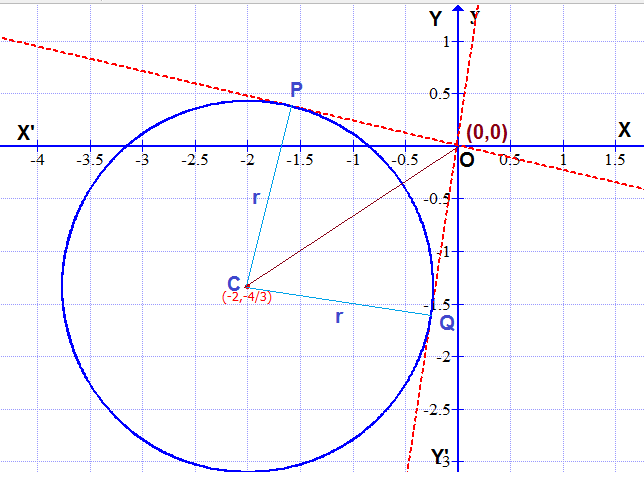
So the center of the circle C #to(-2,-4/3)#

and radius of the circle #rtosqrt(28/9)#

If #PandQ# are points of contact of two tangents drawn from origin #O# to the circle then #DeltasPOCandQOC# will be two congruent right triangles both having common hypotenuse OC.

So #PC=QC=r#

Now #OC^2=(0-(-2))^2+(0-(-4/3))^2#

#=>OC=sqrt(52/9)#

So length of each tangent

#OP=sqrt(OC^2-CP^2)#

#=sqrt(52/9-28/9)#

#=sqrt(8/3)=2sqrt(2/3)=(2sqrt6)/3#

Now #sinanglePOC=(PC)/(OC)#

#=>sinanglePOC=sqrt(28/9)/sqrt(52/9)#

#=>anglePOC=sin^-1(sqrt(7/13))=47.2^@#

So angle between the tangents will be

#anglePOQ=2*anglePOC=94.4^@#

But #angle PCQ=2*angle PCO=2*(90^@-47.2^@)=85.6^@#

Related questions
Impact of this question
2444 views around the world
You can reuse this answer
Creative Commons License