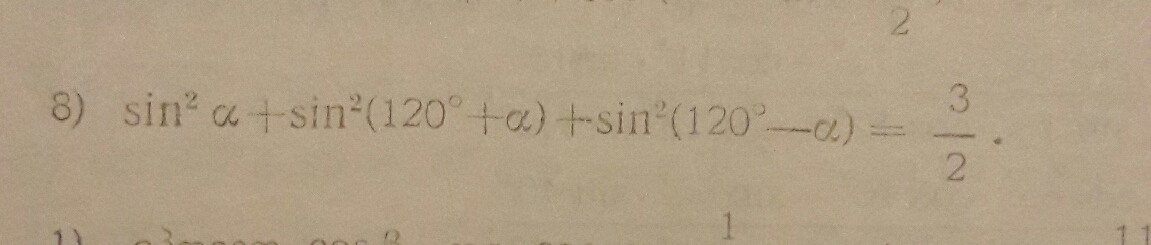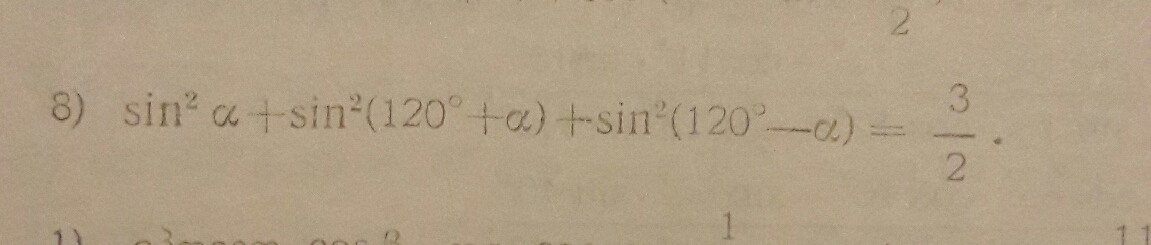sin(120^@+alpha)=sin{180^@-(60^@-alpha)}sin(120∘+α)=sin{180∘−(60∘−α)},
=sin(60^@-alpha)=sin(60∘−α),
=sin60^@cosalpha-cos60^@sinalpha=sin60∘cosα−cos60∘sinα.
rArr sin(120^@+alpha)=1/2(sqrt3cosalpha-sinalpha)......(1).
Similarly, sin(120^@-alpha)=sin(60^@+alpha).
:. sin(120^@-alpha)=1/2(sqrt3cosalpha+sinalpha)......(2).
"From "(1) and (2),
sin^2alpha+sin^2(120^@+alpha)+sin^2(120^@-alpha),
=sin^2alpha+1/4(sqrt3cosalpha-sinalpha)^2+1/4(sqrt3cosalpha+sinalpha)^2,
=sin^2alpha+1/4{2(3cos^2alpha+sin^2alpha)}..........[because, (a+b)^2+(a-b)^2=2(a^2+b^2)],
=sin^2alpha+3/2cos^2alpha+1/2sin^2alpha,
=3/2sin^2alpha+3/2cos^2alpha,
=3/2, as desired!
Spread the Joy of Maths.!